题目内容
19.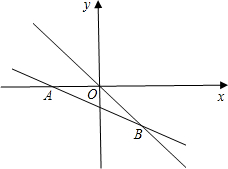 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A,与直线y=-$\frac{\sqrt{3}}{2}$x交于点B.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A,与直线y=-$\frac{\sqrt{3}}{2}$x交于点B.(1)求点B的坐标;
(2)点B关于x轴的对称点为点C,求△AOC的面积;
(3)过点B作BD⊥x轴于点D,动点P从点D出发,在射线DB上以每秒1个单位长度的速度向下运动,运动的时间为t秒,连接OP,将线段OP以点O为旋转中心,逆时针旋转90°得线段OP′,连接AP′,△AP′O的面积为S,在点P运动过程中(不包含点D),S的值是否与t的值有关?如果有关,请直接写出S与t的函数关系式;如果无关,请直接写出S的值.
分析 (1)解两直线的解析式组成的方程组即可求解;
(2)在y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$中令y=0,解得x的值,即可求得A的坐标,然后求得P'的坐标,根据三角形的面积公式即可求解;
(3)作P'E⊥x轴于点E,证明△OPD≌△OP'E,则P'E=OD,根据三角形的面积公式即可求得S.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{5}x-\frac{3\sqrt{3}}{5}}\\{y=-\frac{\sqrt{3}}{2}x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=-\sqrt{3}}\end{array}\right.$,
则B的坐标是(2,-$\sqrt{3}$);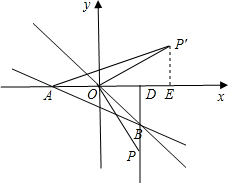
(2)在y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$中令y=0,解得:x=-3,
则A的坐标是(-3,0),
则OA=3.
C的坐标是(2,$\sqrt{3}$),
则S△AOC=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$;
(3)作P'E⊥x轴于点E.
∵P的坐标是(2,-$\sqrt{3}$),PD⊥x轴,
∴D的坐标是(2,0),OD=2.
∵∠POP'=90°,即∠POD+∠P'OE=90°,
又∵直角△ODP中,∠POD+∠OPD=90°,
∴∠P'OE=∠OPD,
∴在△OPD和△OP'E中,$\left\{\begin{array}{l}{∠ODP=∠OEP′}\\{∠P′OE=∠OPD}\\{OP=OP′}\end{array}\right.$,
∴△OPD≌△OP'E,
∴P'E=OD=2.
∴S=S△AP'O=$\frac{1}{2}$OA•P'E=$\frac{1}{2}$×3×2=3.
即S与t无关,S的值是3.
点评 本题是全等三角形的判定以及图形的旋转,一次函数的综合应用,正确作出辅助线,证明△OPD≌△OP'E是关键.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案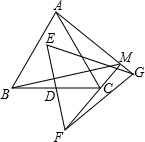 如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$-1 |
老师评分统计表格:
| 评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
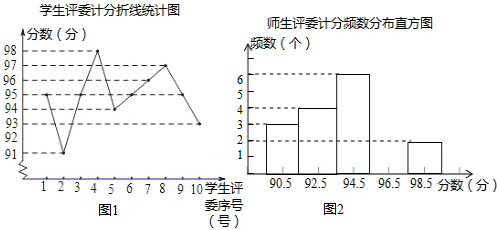
(1)在频数分布直方图中,自左向右第四组的频数为5;
(2)学生评委计分的中位数是95分;
(3)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,别且按老师、学生各占60%、40%的方法计算各班最后得分.已知甲班最后得分为94.4分,求统计表中x的值.
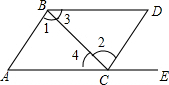 如右图所示,点E在AC的延长线上,如果添一个条件∠3=∠4可以使BD∥AC(只要添一种条件即可)
如右图所示,点E在AC的延长线上,如果添一个条件∠3=∠4可以使BD∥AC(只要添一种条件即可)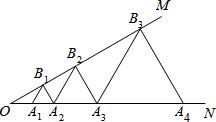 如图,已知,∠MON=30°,点A1,A2,A3在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为8.
如图,已知,∠MON=30°,点A1,A2,A3在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为8.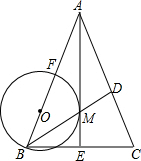 如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.
如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.