题目内容
20.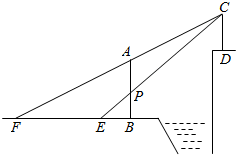 如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,已知:人在塔底B点以西50米的地面E点恰好看到点E、P、C在一直线上,再向西前进150米后从地面F点恰好看到点F、A、C在一直线上,求两铁塔轴线间的距离(即直线AB、CD间的距离)
如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,已知:人在塔底B点以西50米的地面E点恰好看到点E、P、C在一直线上,再向西前进150米后从地面F点恰好看到点F、A、C在一直线上,求两铁塔轴线间的距离(即直线AB、CD间的距离)
分析 延长FB与CD的延长线交于点G,则△BEP∽△GEC,△BFA∽△GFC,根据相似三角形的对应边的比相等即可求解.
解答  解:延长FB与CD的延长线交于点G,则CD⊥FB,AB∥CG.
解:延长FB与CD的延长线交于点G,则CD⊥FB,AB∥CG.
∵AB∥CG,
∴△BEP∽△GEC,
∴$\frac{BE}{EG}=\frac{BP}{CG}$,即$\frac{50}{50+BG}$=$\frac{BP}{CG}$,
同理,$\frac{BF}{FG}=\frac{AB}{CG}$,即$\frac{150+50}{150+50+BG}$=$\frac{2BP}{CG}$,则$\frac{100}{200+BG}=\frac{BP}{CG}$,
∴$\frac{50}{50+BG}$=$\frac{100}{200+BG}$
解得:BG=100.
答:两铁塔轴线间的距离是100米.
点评 本题考查了相似三角形的判定与性质,正确进行比例的变化,转化为方程问题是关键.

练习册系列答案
相关题目
5.对于非零的两个实数a、b,规定a⊕b=$\frac{1}{b}$-$\frac{1}{a}$.若1⊕(x+1)=1,则x的值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
12. 如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )
如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )
 如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )
如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )| A. | 10cm | B. | 9cm | C. | 8cm | D. | 5cm |
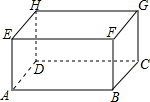 现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.则蜘蛛从表面迅速地捕到小虫的最短路程是$\sqrt{74}$.
现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.则蜘蛛从表面迅速地捕到小虫的最短路程是$\sqrt{74}$. 如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若OB2-AB2=10,则k的值为5.
如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若OB2-AB2=10,则k的值为5.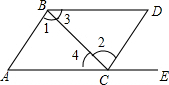 如右图所示,点E在AC的延长线上,如果添一个条件∠3=∠4可以使BD∥AC(只要添一种条件即可)
如右图所示,点E在AC的延长线上,如果添一个条件∠3=∠4可以使BD∥AC(只要添一种条件即可)