题目内容
6.先阅读材料,然后解方程组:材料:解方程组$\left\{\begin{array}{l}{x+y=4①}\\{3(x+y)+y=14②}\end{array}\right.$
在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.
把y=2代入①得x=2,所以$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$
这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组$\left\{\begin{array}{l}{x-y-1=0①}\\{4(x-y)-y=5②}\end{array}\right.$.
分析 根据阅读材料中的方法求出方程组的解即可.
解答 解:由①得:x-y=1③,
把③代入②得:4-y=5,即y=-1,
把y=-1代入③得:x=0,
则方程组的解为$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.以下四个函数,其图象一定关于原点对称的是( )
| A. | y=2016x+m | B. | y=$\frac{x}{2{x}^{2}+1}$+$\frac{m}{x}$ | C. | y=x2-2016 | D. | y=$\frac{{x}^{2}}{|x|}$ |
11.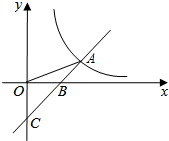 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
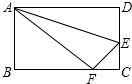 如图,已知矩形ABCD中,AB=8cm,BC=10cm,在边CD上取一点F,将△ADF折叠使点D恰好落在BC边上的点E,则CF的长为4.
如图,已知矩形ABCD中,AB=8cm,BC=10cm,在边CD上取一点F,将△ADF折叠使点D恰好落在BC边上的点E,则CF的长为4. A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t.
A、B两城相距600千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为毎小时100千米,设客车出时间为t.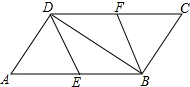 如图,在?ABCD中,点E、F分别为边AB,CD的中点,连接DE,BF,BD.
如图,在?ABCD中,点E、F分别为边AB,CD的中点,连接DE,BF,BD.