题目内容
18.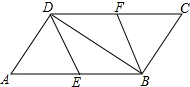 如图,在?ABCD中,点E、F分别为边AB,CD的中点,连接DE,BF,BD.
如图,在?ABCD中,点E、F分别为边AB,CD的中点,连接DE,BF,BD.(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,求证:四边形BFDE为菱形.
分析 (1)根据平行四边形的对边相等的性质可以得到AD=BC,AB=CD,又点E、F是AB、CD中点,所以AE=CF,然后利用边角边即可证明两三角形全等;
(2)先证明BE与DF平行且相等,然后根据一组对边平行且相等的四边形是平行四边形可得四边形BEDF是平行四边形;再根据直角三角形斜边上的中线等于斜边的一半可得DE=EB=$\frac{1}{2}$AB,从而可得四边形BFDE为菱形.
解答 证明:(1)在?ABCD中,AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=$\frac{1}{2}$AB,CF=$\frac{1}{2}$DC,
∴AE=CF,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠C}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SAS);
(2)∵AB=CD,AE=CF,
∴BE=DF,
又AB∥CD,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∵∠ADB=90°,
∴点E为边AB的中点,
∴DE=EB=$\frac{1}{2}$AB,
∴四边形BFDE为菱形.
点评 此题主要考查了菱形的判定,以及全等三角形的判定,关键是掌握一组邻边相等的平行四边形是菱形,直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
9.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.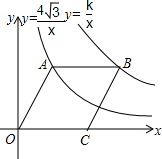 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )| A. | 6$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |