题目内容
15.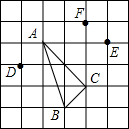 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )| A. | △ACF | B. | △ACE | C. | △ABD | D. | △CEF |
分析 根据全等三角形的对应边相等得到相关线段间的等量关系.然后利用勾股定理进行验证.
解答 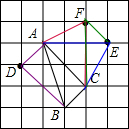 解:在△ABC中,AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,BC=$\sqrt{2}$,AC=2$\sqrt{2}$.
解:在△ABC中,AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,BC=$\sqrt{2}$,AC=2$\sqrt{2}$.
A、在△ACF中,AF=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$≠$\sqrt{10}$,$\sqrt{5}$≠$\sqrt{2}$,$\sqrt{5}$≠2$\sqrt{2}$,则△ACF与△ABC不全等,故本选项错误;
B、在△ACE中,AE=3≠$\sqrt{10}$,3≠$\sqrt{2}$,3≠2$\sqrt{2}$,则△ACE与△ABC不全等,故本选项错误;
C、在△ABD中,AB=AB,AD=$\sqrt{2}$=BC,BD=AC=2$\sqrt{2}$,则由SSS推知△ACF与△ABC全等,故本选项正确;
D、在△CEF中,CF=3≠$\sqrt{10}$,3≠$\sqrt{2}$,3≠2$\sqrt{2}$,则△CEF与△ABC不全等,故本选项错误;
故选:C.
点评 本题考查了勾股定理和全等三角形的判定.此题利用了全等三角形的判定定理SSS进行证明的.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
10.2015年1月24日,“贵广大庙会”在贵阳观山湖区正式面向市民开发,第一次就有近5.6×104人到场购置年货,5.6×104可以表示为( )
| A. | 56 | B. | 560 | C. | 5600 | D. | 56000 |
 选作题(请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.)
选作题(请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.)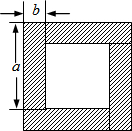 用四块完全相同的小长方形拼成的一个“回形”正方形.
用四块完全相同的小长方形拼成的一个“回形”正方形.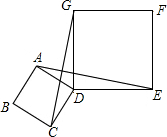 如图,已知四边形ABCD和DEFG都是正方形,连接AE、CG.请猜想AE与CG有什么数量关系?并证明你的猜想.
如图,已知四边形ABCD和DEFG都是正方形,连接AE、CG.请猜想AE与CG有什么数量关系?并证明你的猜想.