题目内容
4.若x等于它的倒数,则$\frac{x+2}{{x}^{2}+6x+9}$÷$\frac{1}{(x-2)(x+3)^{2}}$的值是( )| A. | 0 | B. | -3 | C. | 5 | D. | 7 |
分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x+2}{(x+3)^{2}}$•(x-2)(x+3)2
=x2-4.
∵x等于它的倒数,即x=$\frac{1}{x}$,
∴x2=1,
∴原式=1-4=-3.
故选B.
点评 本题考查的是分式的化简求值,熟知分式混和运算的法则是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.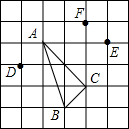 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )| A. | △ACF | B. | △ACE | C. | △ABD | D. | △CEF |
12.零售商小张获得了某公司为期60天的新产品销售权,已知该产品的成本为35元/件,经调查,此商品在第x天的销售量p件与销售天数x的关系如下表:
销售单位q(元/件)与x满足:当1≤x<45时,q=x+55;当45≤x≤60时,q=35+$\frac{2925}{x}$.
(1)请分析表格中销售量p与x的关系,请直接写出销售量p与x的关系;
(2)请求出这60天内小张获得的最大日销售利润;
(3)为调动零售商积极性,公司在销售开始的前45天内,每售出一件商品,公司返m(m≥10)元给零售商,通过调查发现,当x≤30时,小张获得返现后的日销售利润随x的增大而增大,求m的取值范围.
| x(天) | 1 | 2 | 3 | … | 60 |
| p(件) | 198 | 196 | 194 | 80 |
(1)请分析表格中销售量p与x的关系,请直接写出销售量p与x的关系;
(2)请求出这60天内小张获得的最大日销售利润;
(3)为调动零售商积极性,公司在销售开始的前45天内,每售出一件商品,公司返m(m≥10)元给零售商,通过调查发现,当x≤30时,小张获得返现后的日销售利润随x的增大而增大,求m的取值范围.
16.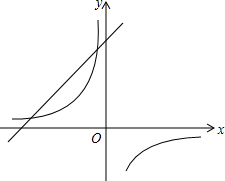 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )| A. | m>2 | B. | m>2且m≠3 | C. | 2<m≤3 | D. | 2<m<3 |
14.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

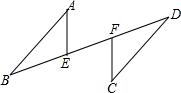 如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).
如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).