题目内容
6.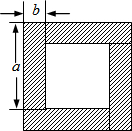 用四块完全相同的小长方形拼成的一个“回形”正方形.
用四块完全相同的小长方形拼成的一个“回形”正方形.(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式,试用乘法公式说明这个等式成立;
(2)利用(1)中的结论计算:a+b=2,ab=$\frac{3}{4}$,求a-b;
(3)根据(1)中的结论,直接写出x+$\frac{1}{x}$和x-$\frac{1}{x}$之间的关系;若x2-3x+1=0,分别求出x+$\frac{1}{x}$和(x-$\frac{1}{x}$)2的值.
分析 (1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积-小正方形的面积,利用完全平方公式,即可解答;
(2)根据完全平方公式解答;
(3)根据完全平分公式解答.
解答 解:(1)阴影部分的面积为:4ab或(a+b)2-(a-b)2,
得到等式:4ab=(a+b)2-(a-b)2,
说明:(a+b)2-(a-b)2=a2+2ab+b2-(a2-2ab+b2)=a2+2ab+b2-a2+2ab-b2=4ab.
(2)(a-b)2=(a+b)2-4ab=${2}^{2}-4×\frac{3}{4}$=4-3=1,
∴a-b=±1.
(3)根据(1)中的结论,可得:$(x-\frac{1}{x})^{2}=(x+\frac{1}{x})^{2}-4$,
∵x2-3x+1=0,
方程两边都除以x得:$x-3+\frac{1}{x}=0$,
∴$x+\frac{1}{x}=3$,
∴$(x-\frac{1}{x})^{2}=(x+\frac{1}{x})^{2}-4={3}^{2}-4=5$.
点评 本题考查了完全平方公式的几何背景,准确识图,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键.

练习册系列答案
相关题目
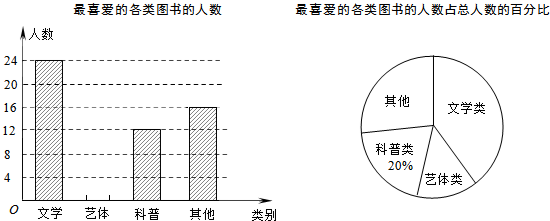
16.某校为了了解学生的体能状况,决定抽取部分同学进行体育测试参加测试的每名学生从“1000米跑步”、“立定跳远”,“1分钟跳绳”、“坐位体前屈”四个项目中随机抽取两项作为测试项目.
(1)求:小明同学恰好抽到“立定跳远”,“坐位体前屈”两项的概率.
(2)据统计,初二三班共10名学生参加了测试,两项的平均成绩如下:
94 100 90 84 92 50 89 64 71 92
①该表是这10名同学平均成绩的一些统计数据,请将表格中缺少的数据补充完整.
②为了调动学生参与体育锻炼的积极性,该班决定对参与测试的同学进行奖励,决定制定一个奖励标准,成绩凡达到或超过这个标准的学生将受到奖励,如果要使参与测试的学生半数左右能获奖,根据上面的计算结果,这个标准应定为多少?并简述理由.
(1)求:小明同学恰好抽到“立定跳远”,“坐位体前屈”两项的概率.
(2)据统计,初二三班共10名学生参加了测试,两项的平均成绩如下:
94 100 90 84 92 50 89 64 71 92
①该表是这10名同学平均成绩的一些统计数据,请将表格中缺少的数据补充完整.
| 平均数 | 中位数 | 众数 |
| 82.6 | 89.5 | 92 |
11.某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张,印刷费与印数的关系见下表:
(1)印制这批纪念册的制版费为1500元;
(2)若印制2千册,则共需多少费用?
| 印数a(单位:千册) | 1≤a<5 | 5≤a<10 |
| 彩色(单位:元/张) | 2.2 | 2.0 |
| 黑白(单位:元/张) | 0.8 | 0.6 |
(2)若印制2千册,则共需多少费用?
18.定义符号max{a,b}的含义为:当a≥b时max{a,b}=a;当a<b时,max{a,b}=b.如:max{1,-3}=1,max{-4,-2}=-2.则max{x2-1,x}的最小值是( )
| A. | 0 | B. | 1 | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\frac{{1-\sqrt{5}}}{2}$ |
15.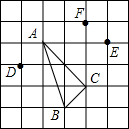 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )| A. | △ACF | B. | △ACE | C. | △ABD | D. | △CEF |
16.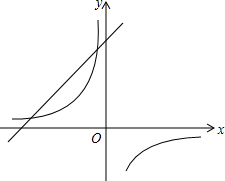 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )| A. | m>2 | B. | m>2且m≠3 | C. | 2<m≤3 | D. | 2<m<3 |