题目内容
5.为了解某一实际问题中变量y(y>0)随变量x(x>0)的变化情况.实验小组在一定条件下,通过一次又一次的实验,测出变量x、y在每一次实验后的一组对应数据如表.(1)根据表中数据猜想变量y(y>0)关于变量x(x>0)的函数关系式,并说明理由;
(2)若80<y<90,请估计x的取值范围.
| x | 100 | 90 | 80 | 70 | 60 |
| y | 60 | 67 | 75 | 86 | 100 |
分析 (1)根据表中的数据,可画出图象,根据图象的形状,选择反比例函数模型进行尝试,再验证即可;
(2)分别求出y=80与y=90时x的值,即可得到80<y<90时x的取值范围.
解答 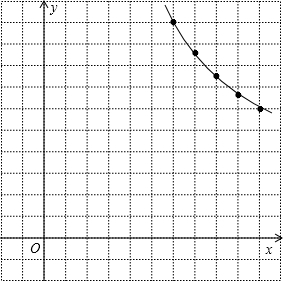 解:(1)如图,猜想变量y(y>0)关于变量x(x>0)的函数关系为反比例函数关系.
解:(1)如图,猜想变量y(y>0)关于变量x(x>0)的函数关系为反比例函数关系.
设它的函数关系式为y=$\frac{k}{x}$(k≠0),
选点(60,100)的坐标代入,求得k=6000,
则y=$\frac{6000}{x}$(x>0).
将点(70,86),(80,75),(90,67),(100,60)的坐标一一代入y=$\frac{6000}{x}$,
验证:$\frac{6000}{70}$≈86,$\frac{6000}{80}$=75,$\frac{6000}{90}$≈67,$\frac{6000}{100}$=60,可见y=$\frac{6000}{x}$(x>0)相当精确反映了函数关系式;
(2)∵y=$\frac{6000}{x}$,
∴当y=80时,x=75;当y=90时,x=66$\frac{2}{3}$,
∴x的取值范围为66$\frac{2}{3}$<x<75.
点评 本题考查了反比例函数的应用,待定系数法求函数的解析式,熟知反比例函数图象的形状判断出y关于x的函数关系为反比例函数关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.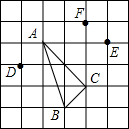 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )| A. | △ACF | B. | △ACE | C. | △ABD | D. | △CEF |
16.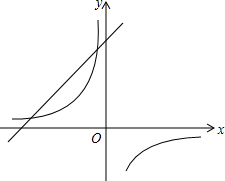 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )| A. | m>2 | B. | m>2且m≠3 | C. | 2<m≤3 | D. | 2<m<3 |
10.把几个数用大括号围起来,中间用逗号断开,如:{1,2,3}、{-2,7,8,19},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当实数a是集合的元素时,实数8-a也必是这个集合的元素,这样的集合我们称为好的集合.下列集合为好的集合的是( )
| A. | {1,2} | B. | {1,4,7} | C. | {1,7,8} | D. | {-2,6} |
14.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |