题目内容
8.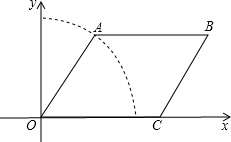 如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.
如图,点A是以O为圆心的圆上的一个动点,点C是x轴正半轴上的一个动点,BC∥OA,AB∥x轴.(1)四边形OABC是平行四边形,这是因为BC∥OA,AB∥x轴;
(2)当点A运动到y轴时,四边形OABC是矩形,这是因为∠AOC=90°;
(3)当点C运动到圆上时,四边形OABC是菱形,这是因为OA=OC.
分析 (1)由两组对边分别平行的四边形为平行四边形,可得出答案;
(2)由条件可知∠AOC=90°,结合(1)可判定其为矩形;
(3)由条件可知OA=OC,结合(1)可判定其为菱形.
解答 解:
(1)∵BC∥OA,AB∥x轴,
∴四边形OABC为平行四边形,
故答案为:平行四边形;BC∥OA,AB∥x轴;
(2)当A运动到y轴时,则∠AOC=90°,
又四边形OABC为平行四边形,
∴四边形OABC为矩形,
故答案为:矩;∠AOC=90°;
(3)当C运动到圆上时,则OA=OC,
又四边形OABC为平行四边形,
∴四边形OABC为菱形,
故答案为:菱;OA=OC.
点评 本题主要考查平行四边形、矩形、菱形的判定,掌握特别四边形的判定方法是解题的关键,注意矩形、菱形都是特殊的平行四边形.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
18.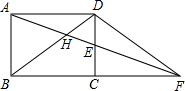 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )| A. | $\frac{10\sqrt{6}}{3}$ | B. | 5$\sqrt{2}$ | C. | 10 | D. | 5 |
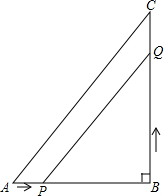 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB方向以1cm/s的速度移动,点Q从点B开始,沿BC方向以2cm/s的速度移动.若点P,Q分别从A点,B点同时出发,几秒钟后,PQ=$\sqrt{5}$AP?
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始,沿AB方向以1cm/s的速度移动,点Q从点B开始,沿BC方向以2cm/s的速度移动.若点P,Q分别从A点,B点同时出发,几秒钟后,PQ=$\sqrt{5}$AP? 如图:已知?ABCD中AE⊥BC于E,AF⊥CD于F,AE=3cm,AF=4cm,CD=8cm,求AD的长.
如图:已知?ABCD中AE⊥BC于E,AF⊥CD于F,AE=3cm,AF=4cm,CD=8cm,求AD的长.