已知BD垂直平分AC.∠BCD=∠ADF.AF⊥AC.求证:四边形ABDF是平行四边形．题目和参考答案——青夏教育精英家教网—

题目内容

17．

已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，求证：四边形ABDF是平行四边形．

分析利用线段垂直平分线的性质得出AB=CB，AD=CD，进而得出AF∥BD，AB∥FD即可证出四边形ABDF是平行四边形．

解答证明：∵BD垂直平分AC，
∴AB=CB，AD=CD，
∴∠BAC=∠BCA，∠DAC=∠DCA．
即∠BAD=∠BCD，
∵∠BCD=∠ADF，
∴∠BAD=∠ADF，
∴AB∥FD，
又∵BD⊥AC，AF⊥AC，
∴AF∥BD，
∴四边形ABDF是平行四边形．

点评此题主要考查了平行四边形的判定，关键是掌握两组对边分别平行的四边形是平行四边形．

练习册系列答案

8．

在正方形ABCD内有一点P，且PA=2$\sqrt{2}$，PB=1，PD=$\sqrt{17}$，则正方形ABCD的边长为$\sqrt{13}$．

5．

如图是一张边长为8的正方形纸片，在正方形纸片上剪下一个腰长为5的等腰三角形（要求：等腰三角形的一个顶点与正方形的一个顶点重合，其余两个顶点在正方形的边上），则剪下的等腰三角形的底边长是（　　）

4$\sqrt{3}$或5$\sqrt{2}$

D．

4$\sqrt{5}$或5$\sqrt{2}$

12．已知点P（x₀，y₀）和直线kx-y+b=0（由y=kx+b变形而得），则点P到直线kx-y+b=0的距离d可用公式d=$\frac{{|{k{x_0}-{y_0}+b}|}}{{\sqrt{1+{k^2}}}}$计算．例如：求点P（-2，1）到直线y=x+1的距离．解：由直线y=x+1可得x-y+1=0，k=1，b=1．则点P到直线y=x+1的距离为d=$\frac{{|{k{x_0}-{y_0}+b}|}}{{\sqrt{1+{k^2}}}}$=$\frac{{|{1×（-2）-1+1}|}}{{\sqrt{1+{1^2}}}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$．根据以上材料，解决下列问题：
（1）请求出点P（1，1）到直线y=3x-12的距离；
（2）已知互相平行的直线y=x-2与y=x+b之间的距离是3$\sqrt{2}$，试求b的值．

2．

如图所示，AH∥DG∥BC，DF∥AC，图中和∠ACB相等的角（不包括自身）有（　　）

9．

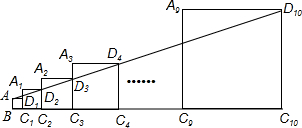已知正方形ABC₁D₁的边长为1，延长C₁D₁到A₁，以A₁C₁为边向右作正方形A₁C₁C₂D₂，延长C₂D₂到A₂，以A₂C₂为边向右作正方形A₂C₂C₃D₃（如图所示），以此类推…．若A₁C₁=2，且点A，D₂，D₃，…，D₁₀都在同一直线上，则正方形A₉C₉C₁₀D₁₀的边长是$\frac{{3}^{8}}{{2}^{7}}$．

6．已知数据：2，4，2，5，7．则这组数据的众数和中位数分别是（　　）

7．

如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA=125°．

试题分类