题目内容
7. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=125°.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=125°.
分析 连接OD,构造直角三角形,利用OA=OD,可求得∠ODA=35°,从而根据∠CDA=∠CDO+∠ODA计算求解.
解答 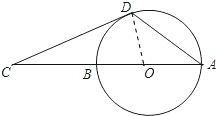 解:连接OD,则∠ODC=90°,∠COD=70°;
解:连接OD,则∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A=$\frac{1}{2}$∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°,
故答案为:125.
点评 本题利用了切线的性质,三角形的外角与内角的关系,等边对等角求解.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
2.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 直角三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 正六边形 |
19. 如图所示,直线a,b被直线c所截,∠1与∠2是( )
如图所示,直线a,b被直线c所截,∠1与∠2是( )
 如图所示,直线a,b被直线c所截,∠1与∠2是( )
如图所示,直线a,b被直线c所截,∠1与∠2是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 邻补角 |
16.若一个等腰三角形的两边长分别是2和5,则它的周长为( )
| A. | 12 | B. | 9 | C. | 12或9 | D. | 9或7 |
17.若(x+2)(x-1)=x2+mx+n,则m+n=( )
| A. | 1 | B. | -2 | C. | -1 | D. | 2 |
 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,求证:四边形ABDF是平行四边形.
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,求证:四边形ABDF是平行四边形.