题目内容
19.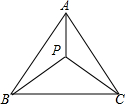 如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.
如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.
分析 如图将△ABP绕点A顺时针旋转60°得到△AEF,连接EB,先说明PA+PB+PC的最小值就是EC的长,根据EC=2EO即可即可解决问题.
解答 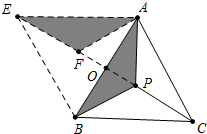 解:如图,将△ABP绕点A顺时针旋转60°得到△AEF,连接EB,则△AEB、△APF是等边三角形,
解:如图,将△ABP绕点A顺时针旋转60°得到△AEF,连接EB,则△AEB、△APF是等边三角形,
此时PA+PB+PC=PC+PF+EF,所以当E、F、P、C共线时,PA+PB+PC最小,这个最小值就是EC的长.
设EC交AB于点O,∵△AEB,△ABC都是边长为4的等边三角形,
∴EC=2EO=2×$\frac{\sqrt{3}}{2}$×4=4$\sqrt{3}$.
故答案为4$\sqrt{3}$.
点评 本题考查等边三角形的性质、轴对称-最短问题,解题的关键是利用旋转添加辅助线找到PA+PB+PC的最小值就是线段EC的长,题目有一点难度,掌握添加辅助线的方法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.
如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.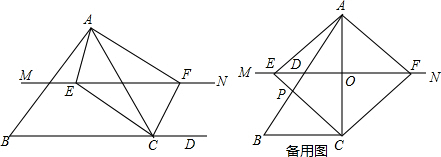
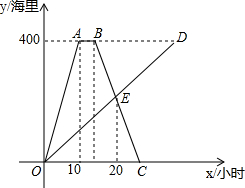 巡洋舰完成某海域巡航任务返回基地补给,同时海警船前往相同海域执怯(巡洋舰与海警船始终在同一航线上航行),巡洋舰返回基地修整5小时后立即按原路原速返回,如图是巡洋舰与海警船离各自出发地的路程y(单位:海里)与海警船航行时间x(单位:时)的承数图象.
巡洋舰完成某海域巡航任务返回基地补给,同时海警船前往相同海域执怯(巡洋舰与海警船始终在同一航线上航行),巡洋舰返回基地修整5小时后立即按原路原速返回,如图是巡洋舰与海警船离各自出发地的路程y(单位:海里)与海警船航行时间x(单位:时)的承数图象.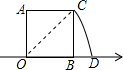 如图,以数轴的单位长线段为边作一个正方形AOBC,以数轴的原点圆心,对角线OC为半径画弧,交数轴于点D,则点D表示的数是$\sqrt{2}$.
如图,以数轴的单位长线段为边作一个正方形AOBC,以数轴的原点圆心,对角线OC为半径画弧,交数轴于点D,则点D表示的数是$\sqrt{2}$.