题目内容
15.已知抛物线y=ax2+bx+c(a>0)的顶点坐标为(-1,-$\frac{16}{5}$),且知关于x的一元二次方程ax2+bx+c=0的一个根是2.5,则另一个根是-4.5.分析 由抛物线的顶点坐标得出对称轴x=-1,根据抛物线与x轴的两个交点到对称轴的距离相等,设另一个交点为(x,0),解得x的值即可.
解答 解:∵抛物线y=ax2+bx+c(a>0)的顶点坐标为(-1,-$\frac{16}{5}$),
∴抛物线的对称轴为x=-1,
∵关于x的一元二次方程ax2+bx+c=0的一个根是2.5,
∴抛物线与x轴的一个交点坐标为(2.5,0),
设抛物线与x轴的另一个交点坐标为:(x,0),
∵抛物线与x轴的两个交点到对称轴的距离相等,
∴$\frac{2.5+x}{2}$=-1,
解得:x=-4.5,
∴抛物线与x轴的另一个交点坐标为:(-4.5,0).
∴关于x的一元二次方程ax2+bx+c=0的另一个根是-4.5;
故答案为:-4.5.
点评 本题考查了求抛物线与x轴的交点问题,关键是掌握抛物线与x轴的两交点关于对称轴对称.

练习册系列答案
相关题目
20.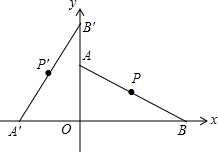 如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
 如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )| A. | (-3,$\sqrt{3}$) | B. | ($-\sqrt{3}$,3) | C. | ($\sqrt{3}$,-3) | D. | (-1,$\sqrt{3}$) |
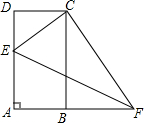 如图,在矩形ABCD中,AD=8,AB=4,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠AFE的余弦值为$\frac{2\sqrt{5}}{5}$.
如图,在矩形ABCD中,AD=8,AB=4,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠AFE的余弦值为$\frac{2\sqrt{5}}{5}$. 如图,?ABCD中,AD=3cm,AB=5cm,BD⊥AD.点P从点A出发,沿AD方向匀速运动,同时点Q从点B出发,沿BA方向匀速运动,它们运动的速度为1cm/s.设运动的时间为x(s),△CPQ的面积为y(cm2),当点Q运动到点A时,P,Q都停止运动.
如图,?ABCD中,AD=3cm,AB=5cm,BD⊥AD.点P从点A出发,沿AD方向匀速运动,同时点Q从点B出发,沿BA方向匀速运动,它们运动的速度为1cm/s.设运动的时间为x(s),△CPQ的面积为y(cm2),当点Q运动到点A时,P,Q都停止运动.