题目内容
12．解方程：$\frac{4+x}{x-1}-5=\frac{2x}{x+1}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：去分母得：x2+5x+4-5x2+5=2x2-2x，
整理得：6x2-7x-9=0，
这里a=6，b=-7，c=-9，
∵△=49+216=265，
∴x=$\frac{7±\sqrt{265}}{12}$，
经检验x=$\frac{7±\sqrt{265}}{12}$都是分式方程的解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程时注意要检验．
练习册系列答案
相关题目
2．
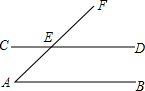如图，直线AB∥CD，AF交CD于点E，∠CEA=45°，则∠A等于（ ）
如图，直线AB∥CD，AF交CD于点E，∠CEA=45°，则∠A等于（ ）| A． | 35° | B． | 45° | C． | 50° | D． | 135° |
如图，?ABCD中，AD=3cm，AB=5cm，BD⊥AD．点P从点A出发，沿AD方向匀速运动，同时点Q从点B出发，沿BA方向匀速运动，它们运动的速度为1cm/s．设运动的时间为x（s），△CPQ的面积为y（cm2），当点Q运动到点A时，P，Q都停止运动．
20．
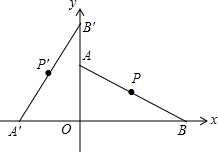如图，在平面直角坐标系中，A（0，$2\sqrt{3}$），B（6，0），点P为线段AB的中点，将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是（ ）
如图，在平面直角坐标系中，A（0，$2\sqrt{3}$），B（6，0），点P为线段AB的中点，将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是（ ）| A． | （-3，$\sqrt{3}$） | B． | （$-\sqrt{3}$，3） | C． | （$\sqrt{3}$，-3） | D． | （-1，$\sqrt{3}$） |
17．已知反比例函数y=-$\frac{3}{x}$，下列结论不正确的是（ ）
| A． | 图象必经过点（-1，3） | B． | 两个分支分布在第二、四象限 | ||
| C． | 若x＞1，则-3＜y＜0 | D． | y随x的增大而增大 |
12．
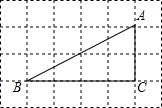如图，△ABC的顶点都是正方形网格中的格点，则cosA等于（ ）
如图，△ABC的顶点都是正方形网格中的格点，则cosA等于（ ）| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\sqrt{5}$ | D． | $\frac{2}{3}$ |