题目内容
16.甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒钟跑6米,甲的速度是乙速度的三分之四倍.(1)如果甲、乙两人在跑道上相距50米处同时反向出发,那么经过多少秒两人第二次相遇?
(2)如果甲在乙的前50米处同时同向出发,那么经过多少秒两人首次相遇?第二次相遇呢?
分析 (1)设再经过x秒甲、乙两人相遇,根据甲、乙所跑的距离和等于400-50+400=750米列方程求解;
(2)先设经过y秒两人首次相遇,这时甲比乙多跑400-50=350米,据此列方程求出答案即可;
设经过t秒后两人第二次相遇,这时甲比乙多跑400-50+400=750米,利用路程差列方程求解.
解答 解:(1)设再经过x秒甲、乙两人相遇,由题意得
6×$\frac{4}{3}$x+6x=400-50+400,
解得:x=53$\frac{4}{7}$.
答:经过53$\frac{4}{7}$秒两人第二次相遇;
(2)先设经过y秒两人首次相遇,由题意得
6×$\frac{4}{3}$y-6y=400-50,
解得:y=175.
答:经过175秒两人首次相遇;
设经过t秒后两人第二次相遇,
6×$\frac{4}{3}$t-6t=400-50+400,
解得:t=375.
答:经过375秒两人第二次相遇.
点评 此题考查一元一次方程的实际运用,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
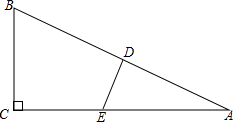 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=30°,且CE=2cm,求AC的长.
如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=30°,且CE=2cm,求AC的长.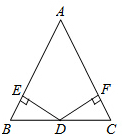 如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.
如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.