题目内容
9.已知10m=20,10n=$\frac{1}{5}$,你能求出32n÷9m的值吗?分析 根据幂的乘方,可得同底数幂的除法,根据同底数幂的除法,可得答案.
解答 解:能求出32n÷9m的值,过程如下:
10n-m=10n÷10m=$\frac{1}{5}$÷20=$\frac{1}{100}$=10-2,
n-m=-2.
32n÷9m=9n÷9m=9n-m=9-2=$\frac{1}{{9}^{2}}$=$\frac{1}{81}$.
点评 本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.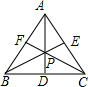 在△ABC中,∠B、∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )
在△ABC中,∠B、∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )
 在△ABC中,∠B、∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )
在△ABC中,∠B、∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 等腰三角形 |
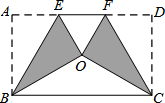 将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$.
将矩形纸片ABCD按如图方式折叠,BE、CF为折痕,折叠后点A和点D都落在点O处,若△EOF是等边三角形,则$\frac{AB}{AD}$的值为$\frac{\sqrt{3}}{3}$. 实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.
实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.