题目内容
17.计算:(2$\sqrt{\frac{3}{7}}$)2=$\frac{12}{7}$,-$\sqrt{(-5\frac{1}{2})^{2}}$=-5$\frac{1}{2}$.分析 先根据积的乘方进行计算,再求出即可;根据二次根式的性质进行化简.
解答 解:(2$\sqrt{\frac{3}{7}}$)2=4×$\frac{3}{7}$=$\frac{12}{7}$,
-$\sqrt{(-5\frac{1}{2})^{2}}$=-5$\frac{1}{2}$,
故答案为:$\frac{12}{7}$,-5$\frac{1}{2}$.
点评 本题考查了二次根式的性质和二次根式的乘除法等知识点能灵活运用知识点进行计算是解此题的关键.

练习册系列答案
相关题目
6.在表中,我们把第i行第j列的数记为ai,j(其中i,j都是不大于4的正整数),对于表中的每个数ai,j,规定如下:当i>j时,ai,j=0;当i≤j时,ai,j=1.
例如:当i=4,j=1时,ai,j=a4,1=0.
(1)按此规定a1,3=1;
(2)请从下面两个问题中任选一个作答.
例如:当i=4,j=1时,ai,j=a4,1=0.
| a1,1 | a1,2 | a1,3 | a1,4 |
| a2,1 | a2,2 | a2,3 | a2,4 |
| a3,1 | a3,2 | a3,3 | a3,4 |
| a4,1 | a4,2 | a4,3 | a4,4 |
(2)请从下面两个问题中任选一个作答.
| 问题1 | 问题2 |
| a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0或3; | 表中的16个数中,共有10个1. |
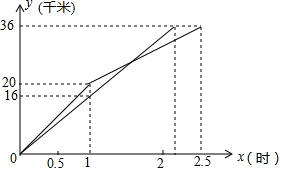 一次国际龙舟拉力赛中,上午9时,参赛龙舟同时出发,其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.
一次国际龙舟拉力赛中,上午9时,参赛龙舟同时出发,其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点. 如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=$\frac{1}{2}$,cot∠ABC=$\frac{3}{4}$,AD=8.
如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=$\frac{1}{2}$,cot∠ABC=$\frac{3}{4}$,AD=8. 如图,已知∠1=70°,∠2=110°,那么AB与CD平行吗?为什么?
如图,已知∠1=70°,∠2=110°,那么AB与CD平行吗?为什么?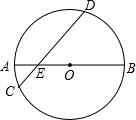 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长.