题目内容
19.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,若原来点A坐标是(a,b),则经过第2015次变换后所得的A点坐标是多少?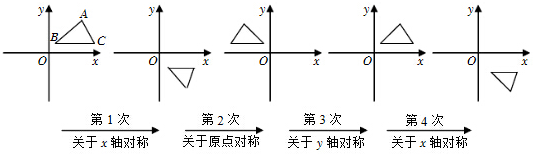
分析 根据关于x轴对称的点的横坐标相同,纵坐标互为相反数,关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,关于y轴对称的点横坐标互为相反数,纵坐标相等,可得规律:每三次以循环,根据规律:(a,-b),((-a,b),(a,b),可得答案.
解答 解:(a,b)关于x轴对称(a,-b),
关于远点对称(-a,b),
关于y轴对称(a,b),
每三次以循环.
2015÷3=671…2
即第672轮的第二次,
经过第2015次变换后所得的A点坐标是(-a,b).
点评 本题考查了几何变换的类型,熟记关于x轴对称的点的横坐标相同,纵坐标互为相反数,关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,关于y轴对称的点横坐标互为相反数,纵坐标相等是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
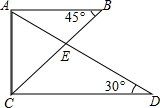 将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.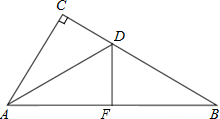 如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长.
如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长. 如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.
如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.