题目内容
9. 如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.
如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.
分析 根据角平分线的定义可得∠ADP=∠PDF,∠CBP=∠PBA,再根据三角形的内角和定理和三角形的外角的性质列出等式整理即可.
解答 解:∵BP平分∠ABC,DP平分∠ADC,
∴∠ADP=∠PDC,∠CBP=∠PBA,
∵∠A+∠ABP=∠P+∠ADP,
∠C+∠CDP=∠P+∠PBC,
∴∠A+∠C=2∠P,
∵∠A=40°,∠C=76°,
∴∠P=$\frac{1}{2}$(40°+76°)=58°.
点评 本题考查了三角形的内角和定理,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
1.科研人员在测试一枚火箭竖直向上升空时发现,火箭的高度h(m)与时间t(s)的关系数据如下:
(1)根据上表,以时间t为横轴,高度h为纵轴建立直角坐标系,并描出上述各点;
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
| 时间t/s | 1 | 5 | 10 | 15 | 20 | 25 |
| 火箭高度h/m | 155 | 635 | 1010 | 1135 | 1010 | 635 |
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
 如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.
如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积. 如图,在五边形ABCDE中,AB∥CD,∠A=125°,∠D=150°,求∠E的度数.
如图,在五边形ABCDE中,AB∥CD,∠A=125°,∠D=150°,求∠E的度数.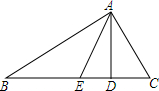 如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.
如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.