题目内容
11.已知等腰△ABC的两边长分别是4和9,等腰△DEF的腰长为6,则当它的底边长为$\frac{8}{3}$时,等腰△ABC和等腰△DEF相似.分析 由题意得出等腰△ABC的腰长是9,底边长为4,当$\frac{AB}{DE}=\frac{BC}{EF}$时,△ABC∽△DEF,即$\frac{9}{6}=\frac{4}{EF}$,即可得出结果.
解答 解:如图所示: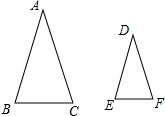
∵等腰△ABC的两边长分别是4和9,4+4<9,
∴等腰△ABC的腰长是9,底边长为4,
∵等腰△DEF的腰长为6,
∴当$\frac{AB}{DE}=\frac{BC}{EF}$时,△ABC∽△DEF,
即$\frac{9}{6}=\frac{4}{EF}$,
∴EF=$\frac{8}{3}$,
即等腰△DEF的腰长为6,则当它的底边长为$\frac{8}{3}$时,等腰△ABC和等腰△DEF相似;
故答案为:$\frac{8}{3}$.
点评 本题考查了等腰三角形的性质、相似三角形的判定、三角形的三边关系;熟练掌握等腰三角形的性质,由腰长与底边成比例求出底边长是解决问题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
1.科研人员在测试一枚火箭竖直向上升空时发现,火箭的高度h(m)与时间t(s)的关系数据如下:
(1)根据上表,以时间t为横轴,高度h为纵轴建立直角坐标系,并描出上述各点;
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
| 时间t/s | 1 | 5 | 10 | 15 | 20 | 25 |
| 火箭高度h/m | 155 | 635 | 1010 | 1135 | 1010 | 635 |
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
 如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠α的度数为100度.
如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠α的度数为100度. 已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.
已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.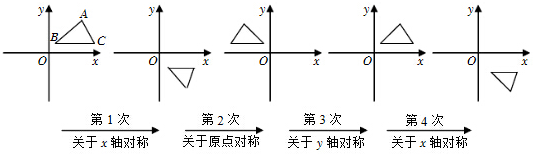
 如图 在△ABC中,∠B=90° AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动. 如果P,Q分别从A,B同时出发 那么△PBQ的面积S随出发的时间t如何变化?写出函数关系式.并指出几秒后△PBQ的面积最大,最大面积是多少?
如图 在△ABC中,∠B=90° AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动. 如果P,Q分别从A,B同时出发 那么△PBQ的面积S随出发的时间t如何变化?写出函数关系式.并指出几秒后△PBQ的面积最大,最大面积是多少? 如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.
如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.