题目内容
10.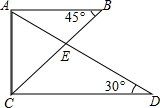 将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.
分析 由∠BAC=∠ACD=90°,可得AB∥CD,即可证得△ABE∽△DCE,然后由相似三角形的对应边成比例,可得:$\frac{BE}{CE}$=$\frac{AB}{CD}$,然后利用三角函数,用AC表示出AB与CD,即可求得答案.
解答 解:∵∠BAC=∠ACD=90°,
∴AB∥CD,
∴△ABE∽△DCE,
∴$\frac{BE}{CE}$=$\frac{AB}{CD}$,
∵在Rt△ACB中∠B=45°,
∴AB=AC,
∵在Rt△ACD中,∠D=30°,
∴CD=$\frac{AC}{tan30°}$=$\sqrt{3}$AC,
∴$\frac{BE}{CE}$=$\frac{AC}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{BE}{CE}$=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{{\sqrt{3}}}{3}$.
点评 此题考查了相似三角形的判定与性质与三角函数的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠α的度数为100度.
如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠α的度数为100度. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒. 已知A、B两点的坐标,如图所示,求△OAB的面积.
已知A、B两点的坐标,如图所示,求△OAB的面积. 已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.
已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.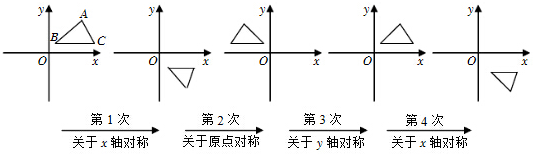
 如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.
如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.