题目内容
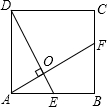 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则| AO |
| DO |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:先证明△AOE∽△DOA,得出AO:DO=AE:AD,再由AE=
AB=
AD,即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠DAO+∠EAO=90°,
∵E为AB的中点,
∴AE=
AB=
AD,
∵AF⊥DE,
∴∠AOE=∠DOA=90°,
∴∠DAO+∠ADO=90°,
∴∠EAO=∠ADO,
∴△AOE∽△DOA,
∴
=
=
.
故选:A
∴AB=AD,∠BAD=90°,
∴∠DAO+∠EAO=90°,
∵E为AB的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AF⊥DE,
∴∠AOE=∠DOA=90°,
∴∠DAO+∠ADO=90°,
∴∠EAO=∠ADO,
∴△AOE∽△DOA,
∴
| AO |
| DO |
| AE |
| AD |
| 1 |
| 2 |
故选:A
点评:本题考查了正方形的性质和相似三角形的判定与性质,证明三角形相似是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
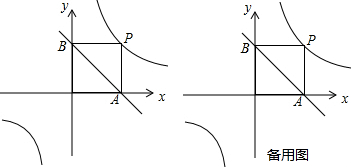
把27430用科学记数法表示应是( )
| A、0.2743×103 |
| B、27.43×103 |
| C、274.3×10 |
| D、2.743×104 |
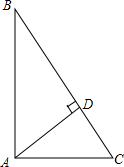 如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,AB=4,DC=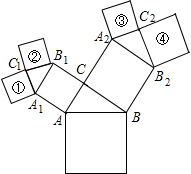 如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.
如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.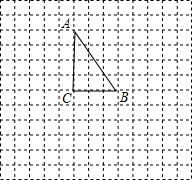 如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.
如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.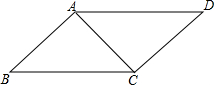 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,
如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm, 如图,在?ABCD中,点E是AD的中点,连接CE、BD相交于点F,则△DEF的周长与△BCF的周长之比C△DEF:C△BCF=
如图,在?ABCD中,点E是AD的中点,连接CE、BD相交于点F,则△DEF的周长与△BCF的周长之比C△DEF:C△BCF=