题目内容
已知(x-z)2-4(x-y)(y-z)=0,且x+z=5,求y的值.
考点:因式分解的应用
专题:
分析:把已知(x-z)2-4(x-y)(y-z)进行因式分解可得(x-2y+z)2,再结合x+z=5可求得y的值.
解答:解:
因为(x-z)2-4(x-y)(y-z)
=(x-y+y+z)2-4(x-y)(y-z)
=(x-y)2+(y-z)2-2(x-y)(y-z)
=(x-y-y+z)2
=0,
所以x+z-2y=0,
又x+z=5,
所以y=2.5.
因为(x-z)2-4(x-y)(y-z)
=(x-y+y+z)2-4(x-y)(y-z)
=(x-y)2+(y-z)2-2(x-y)(y-z)
=(x-y-y+z)2
=0,
所以x+z-2y=0,
又x+z=5,
所以y=2.5.
点评:本题主要考查因式分解的应用,解题的关键是把所给等式左边进行因式分解后得到x+z-2y=0.

练习册系列答案
相关题目
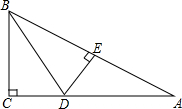 如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比.
如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,作DE⊥AB于点E.若△BCD与△ABC的面积之比为3:8,求△ADE与△ABC的面积之比. 如图,在△ABC中,已知AB=AC,∠BAC=120°,AD是底边BC上的高,求AD:BC的值.
如图,在△ABC中,已知AB=AC,∠BAC=120°,AD是底边BC上的高,求AD:BC的值.