Question

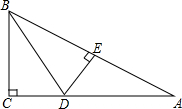如图所示，在△ABC中，∠C=90°，BD平分∠ABC交AC于点D，作DE⊥AB于点E．若△BCD与△ABC的面积之比为3：8，求△ADE与△ABC的面积之比．

Answer 1

考点：角平分线的性质

专题：

分析：求出∠CBD=∠EBD，∠C=∠BED=90°，证△BCD≌△BED，推出△CBD和△EBD的面积相等，求出四边形BCDE与△ABC的面积之比为6：8=3：4，即可得出答案．

解答：解：∵在△ABC中，∠C=90°，BD平分∠ABC交AC于点D，DE⊥AB，
∴∠CBD=∠EBD，∠C=∠BED=90°，
在△BCD和△BED中，

∠C=∠BED ∠CBD=∠EBD BD=BD

，
∴△BCD≌△BED（AAS），
∴△CBD和△EBD的面积相等，
∵△BCD与△ABC的面积之比为3：8，
∴四边形BCDE与△ABC的面积之比为6：8=3：4，
∴△ADE与△ABC的面积之比为1：4．

点评：本题考查了角平分线的性质，全等三角形的面积的应用，解此题的关键是求出四边形BCDE与△ABC的面积之比为6：8．