题目内容
在△ABC中,AB=4,AC=3,BC=5,P是∠A外角平分线上的一点,连接BP、PC,若PC<3,求BP2的长.
考点:正方形的判定与性质,勾股定理,勾股定理的逆定理
专题:
分析:过C点作DC⊥AC交∠A外角平分线于D,过D作DE⊥AB于E,先求得△ABC是直角三角形,AB⊥AC,再根据△ACD和△AED是等腰直角三角形,证得四边形ACDE是正方形,从而求得CD=DE=AE=AC=3,BE=7,根据勾股定理求得BD2=AE2+ED2=72+32=58,由于PC<3=AC=CD,则P应是线段AD上的点,且不与A、D重合,所以AB<BP<BD,进而求得16<BP2<58.
解答: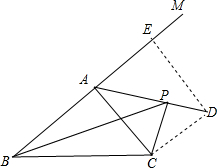 解:过C点作DC⊥AC交∠A外角平分线于D,过D作DE⊥AB于E,
解:过C点作DC⊥AC交∠A外角平分线于D,过D作DE⊥AB于E,
∵AB=4,AC=3,BC=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,AB⊥AC,
∵AP平分∠PAE,
∴∠CAP=∠EAP=45°,
∴△ACD和△AED是等腰直角三角形,
∴四边形ACDE是正方形,
∴CD=DE=AE=AC=3,BE=AB+BE=7,
∴BD2=AE2+ED2=72+32=58,
∵PC<3=AC=CD,
∴P点是线段AD上且不与A、D重合的点,
∴AB<BP<BD,
∴AB2<BP2<BD2,
即16<BP2<58.
 解:过C点作DC⊥AC交∠A外角平分线于D,过D作DE⊥AB于E,
解:过C点作DC⊥AC交∠A外角平分线于D,过D作DE⊥AB于E,∵AB=4,AC=3,BC=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,AB⊥AC,
∵AP平分∠PAE,
∴∠CAP=∠EAP=45°,
∴△ACD和△AED是等腰直角三角形,
∴四边形ACDE是正方形,
∴CD=DE=AE=AC=3,BE=AB+BE=7,
∴BD2=AE2+ED2=72+32=58,
∵PC<3=AC=CD,
∴P点是线段AD上且不与A、D重合的点,
∴AB<BP<BD,
∴AB2<BP2<BD2,
即16<BP2<58.
点评:本题考查了正方形的判定和性质,勾股定理以及勾股定理的逆定理,作出辅助线构建正方形是本题的关键.

练习册系列答案
相关题目
 已知⊙0的直径AB=10,有一动点C从A点沿圆周顺时针运动到点B,若点D为
已知⊙0的直径AB=10,有一动点C从A点沿圆周顺时针运动到点B,若点D为
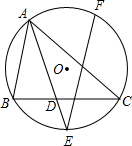 如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.
如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.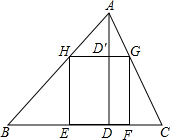 在一底为8米,高为6米的三角形钢板上剪一个面积最大的矩形.
在一底为8米,高为6米的三角形钢板上剪一个面积最大的矩形.