题目内容
16．
如图，把一张长方形的纸片按如图所示样子折叠，则重合部分△DEB的是什么形状，并说明理由．
分析 欲证△BED是等腰三角形，又已知AD∥BC，由折叠可知，∠CBD=∠C′BD，可利用三角形中两内角相等来证等腰．
解答 解：重合部分是等腰三角形．
由折叠可知，∠CBD=∠C′BD，
又∵AD∥BC，
∴∠ADB=∠CBD，
∴∠ADB=∠C′BD，
∴BE=ED．
∴△BED是等腰三角形．
点评 本题考查了图形的折叠，解题过程中注意以下三点：（1）折叠时重合的图形全等；（2）两直线平行的性质；（3）等腰三角形的判定．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
18．
用10米长的铝材制成一个面积为6平方米的窗框，窗框的形状如图所示，若设它的一条竖直方向的边长为x米，则所列方程为（ ）
用10米长的铝材制成一个面积为6平方米的窗框，窗框的形状如图所示，若设它的一条竖直方向的边长为x米，则所列方程为（ ）| A． | x（5-$\frac{3}{2}$x）=6 | B． | x（5-x）=6 | C． | x（10-$\frac{3}{2}$x）=6 | D． | x（10-3x）=6 |
7．
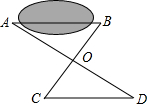要测量池塘的宽度AB，画出如图所示的两个三角形，下面测出的哪组条件不能使CD=AB（ ）
要测量池塘的宽度AB，画出如图所示的两个三角形，下面测出的哪组条件不能使CD=AB（ ）| A． | OA=OD，OB=OC | B． | ∠B=∠C，OB=OC | C． | ∠B=∠C，OA=OD | D． | ∠C=∠B，∠A=∠D |
4．
已知：如图，在△ABC中，∠ACB=90°，CD是边AB上的高，∠A=30°，则线段AB与BD的数量关系是（ ）
已知：如图，在△ABC中，∠ACB=90°，CD是边AB上的高，∠A=30°，则线段AB与BD的数量关系是（ ）| A． | AB=2BD | B． | AB=3BD | C． | AB=4BD | D． | AB=5BD |
如图，在△ABC中，M，N分别是边AB，AC的中点，则△AMN的面积与四边形MBCN的面积比为1：3．
如图，等腰△ABC中，∠CAB=∠CBA，点C、D、E在直线l上，且∠ADC=∠ACB=∠BEC．
6．一元二次方程3x（x+1）=3x+3的解为（ ）
| A． | x=1 | B． | x=-1 | C． | x1=1，x2=-1 | D． | x1=0，x2=-1 |