题目内容
8. 如图,等腰△ABC中,∠CAB=∠CBA,点C、D、E在直线l上,且∠ADC=∠ACB=∠BEC.
如图,等腰△ABC中,∠CAB=∠CBA,点C、D、E在直线l上,且∠ADC=∠ACB=∠BEC.求证:△ADC≌△CEB.
分析 由外角的性质可求得∠BCE=∠CAD,结合条件可证明△ADC≌△CEB.
解答 解:
∵∠CAB=∠CBA,
∴AC=BC,
∵∠ADC=∠ACB=∠BEC,∠ACE=∠ADC+∠DAC,
∴∠ACB+∠BCE=∠DAC+∠ADC,
∴∠DAC=∠BCE,
在△ADC和△CEB中
$\left\{\begin{array}{l}{∠DAC=∠ECB}\\{∠ADC=∠CEB}\\{AC=BC}\end{array}\right.$
∴△ADC≌△CEB(AAS).
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
19.甲、乙、丙三家超市对一种定价相同的商品进行促销.甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次性降价30%.那么顾客购买这种商品应该去的超市是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 一样 |
13.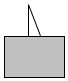 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )| A. | 一个锐角 一个钝角 | B. | 两个锐角 | ||
| C. | 一个锐角 一个直角 | D. | 一个直角 一个钝角 |

 如图,把一张长方形的纸片按如图所示样子折叠,则重合部分△DEB的是什么形状,并说明理由.
如图,把一张长方形的纸片按如图所示样子折叠,则重合部分△DEB的是什么形状,并说明理由. 图中所示为两幅形状相似的油画A和B,它们的对角线分别长42cm和48cm.问油画A的面积是油画B的百分之几?
图中所示为两幅形状相似的油画A和B,它们的对角线分别长42cm和48cm.问油画A的面积是油画B的百分之几? 如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.