题目内容
7.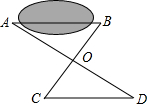 要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )| A. | OA=OD,OB=OC | B. | ∠B=∠C,OB=OC | C. | ∠B=∠C,OA=OD | D. | ∠C=∠B,∠A=∠D |
分析 利用“边角边”证明△ABO和△CDO全等,再根据全等三角形对应边相等可得CD=AB.
解答 解:A、在△ABO和△CDO中,
$\left\{\begin{array}{l}{OA=OD}\\{∠AOB=∠DOC}\\{OB=OC}\end{array}\right.$,
∴△ABO≌△CDO(SAS),
∴CD=AB,不符合题意;
B、在△ABO和△CDO中,
$\left\{\begin{array}{l}{∠B=∠C}\\{OB=OC}\\{∠AOB=∠DOC}\end{array}\right.$,
∴△ABO≌△CDO(ASA),
∴CD=AB,不符合题意;
C、在△ABO和△CDO中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠AOB=∠DOC}\\{OA=OD}\end{array}\right.$,
∴△ABO≌△CDO(AAS),
∴CD=AB,不符合题意;
D、不能利用AAA证明△ABO和△CDO全等,符合题意,
故选D
点评 本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
7.下列各式中一定为负数的是( )
| A. | -(-1) | B. | -|-1| | C. | -(-1)3 | D. | (-1)2 |
2.若有理数a2>b2,则( )
| A. | a>b | B. | a<b | C. | a不小于b | D. | 不能唯一确定 |
12.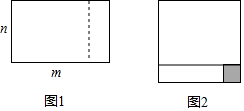 如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )
如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )
 如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )
如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )| A. | 图2所示的长方形是正方形 | |
| B. | 图2所示的长方形周长=2m+2n | |
| C. | 阴影部分所表示的小正方形边长=m-n | |
| D. | 阴影部分所表示的小正方形面积=$\frac{(m-n)^{2}}{4}$ |

 如图,把一张长方形的纸片按如图所示样子折叠,则重合部分△DEB的是什么形状,并说明理由.
如图,把一张长方形的纸片按如图所示样子折叠,则重合部分△DEB的是什么形状,并说明理由. 如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.