Question

2．如图，四边形ABCD是正方形，△ABE是等边三角形，EC=$2\sqrt{3}-2$，则正方形ABCD的面积为8．

Answer 1

分析 过点E作MN∥AD，交AB于点M，交CD于点N，设正方形的边长为a，根据正方形和等边三角形的性质可得出EN、NC的长度，根据勾股定理即可得出关于a的方程，解方程即可得出结论．

解答 解：过点E作MN∥AD，交AB于点M，交CD于点N，如图所示．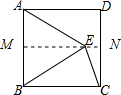
设正方形的边长为a，则ME=$\frac{\sqrt{3}}{2}$a，NC=$\frac{1}{2}$a，EN=AD-ME=a-$\frac{\sqrt{3}}{2}$a，
在Rt△ENC中，由勾股定理得：
EC²=NC²+EN²，即$（2\sqrt{3}-2）^{2}$=$（a-\frac{\sqrt{3}}{2}a）^{2}$+$\frac{1}{4}{a}^{2}$，
解得：a²=8．
故答案为：8．

点评 本题考查了正方形的性质以及等边三角形的性质，解题的关键是找出关于a的方程．本题属于基础题，难度不大，解决该题型题目时，在直角三角形中利用沟谷定理找出关于未知数a的方程是关键．