题目内容
7．函数$y=\sqrt{5-x}+3$ 中，自变量x的取值范围是x≤5．分析 根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．
解答 解：由$y=\sqrt{5-x}+3$ 有意义，得
5-x≥0．
解得x≤5，
故答案为：x≤5．
点评 本题考查了函数自变量的取值范围，函数自变量的范围一般从三个方面考虑：当函数表达式是整式时，自变量可取全体实数；当函数表达式是分式时，考虑分式的分母不能为0；当函数表达式是二次根式时，被开方数非负．
练习册系列答案
相关题目
已知：A、B两市相距260千米，甲车从A市前往B市运送物资，行驶2小时在M地汽车出现故障，立即通知技术人员乘乙车从A市赶来维修（通知时间忽略不计），乙车到达M地后又经过20分钟修好甲车后以原速原路返回，同时甲车以原速1.5倍的速度前往B市，如图是两车距A市的路程y（千米）与甲车行驶时间x（小时）之间的函数图象，由图象信息得出如下结论：①甲车提速后的速度是60千米/时；②乙车的速度是96千米/时；③点C的坐标为（$\frac{19}{6}$，80）；④甲车到达B市时乙车已返回A市2小时．你认为正确的结论有（ ）个．
12．
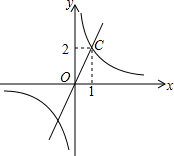反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示．由此可以得到方程$\frac{k}{x}$﹦mx的实数根为（ ）
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示．由此可以得到方程$\frac{k}{x}$﹦mx的实数根为（ ）| A． | x=1 | B． | x=2 | C． | x1=1，x2=-1 | D． | x1=1，x2=-2 |
19．
已知二次函数y=x2-5x+6，当自变量x取m时，对应的函数值小于0，当自变量x取m-1、m+1时，对应的函数值为y1、y2，则y1、y2满足（ ）
已知二次函数y=x2-5x+6，当自变量x取m时，对应的函数值小于0，当自变量x取m-1、m+1时，对应的函数值为y1、y2，则y1、y2满足（ ）| A． | y1＞0，y2＞0 | B． | y1＜0，y2＞0 | C． | y1＜0，y2＜0 | D． | y1＞0，y2＜0 |
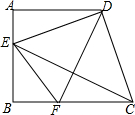如图，已知在梯形ABCD中，AD∥BC，∠A=90°，AB=AD，点E在边AB上，且DE⊥CD，DF平分∠EDC，交BC于点F，联结CE、EF．
17．
如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则$\frac{AM}{MD}$等于（ ）
如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则$\frac{AM}{MD}$等于（ ）| A． | $\frac{3}{8}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |