题目内容
17.已知a-b=4,ab=5,求:(1)a2+b2
(2)(a+b)2.
分析 (1)先根据完全平方公式进行变形,再代入求出即可;
(2)先根据完全平方公式展开,再代入求出即可.
解答 解:(1)∵a-b=4,ab=5,
∴a2+b2=(a-b)2+2ab=42+2×5=26;
(2)∵ab=5,a2+b2=26,
∴(a+b)2=a2+b2+2ab=26+2×5=36.
点评 本题考查了完全平方公式,能灵活根据公式进行变形是解此题的关键.

练习册系列答案
相关题目
6.如图(1),在边长为a的大正方形上剪去一个边长为b的小正方形,可以拼出图(2)所示图形,上述过程可以验证等式( )
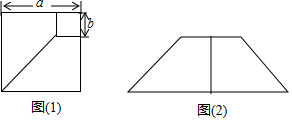

| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
7.为宣传2022年北京-张家口冬季奥运会,小王在网上销售一种成本为20元/件的本届冬季奥运会宣传文化衫,销售过程中的其他各种费用(不再含文化衫成本)总计50(百元),有关销售量y(百件)与销售价格x(元/件)的相关信息如下:
(1)求销售这种文化衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
| 销售量y(百件) | y=-0.1x+8 | y=$\frac{120}{x}$ |
| 销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
 如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°. 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.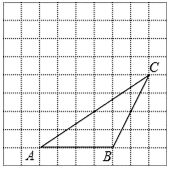 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.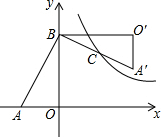 如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=6.
如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=6. 如图,大圆的半径R=10,小圆的半径r=6,大圆的弦AB与小圆相切于点P,有一以点O为圆心的圆面积恰好等于圆环的面积,则它的半径等于8.
如图,大圆的半径R=10,小圆的半径r=6,大圆的弦AB与小圆相切于点P,有一以点O为圆心的圆面积恰好等于圆环的面积,则它的半径等于8.