题目内容
18.如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点Q.(1)求证:CQ=QP
(2)设点Q的坐标为(x,y),求y关于x的函数关系式及自变量x的取值范围;
(3)如图2,连结OQ,OB,当点P在线段OA上运动时,设三角形OBQ的面积为S,当x取何值时,S取得最小值,并求出最小值;
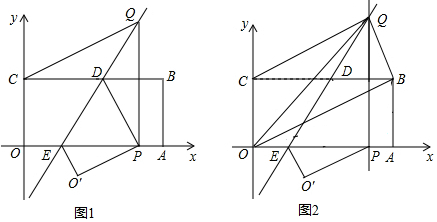
分析 (1)根据SAS证明△CDQ≌△PDQ,则CQ=PQ;
(2)根据Q(x,y)表示QH=y-2,CH=x,在Rt△CQH中,由勾股定理列式得:x2+(y-2)2=y2,化简可得结论,因为P在线段OA,且OA=4,又因为折痕所在直线与OA相交,即OP最小为2,所以2≤x≤4;
(3)先求直线OB的解析式为:y=$\frac{1}{2}$x,设直线OB与直线PQ相交于点G,设G(x,y),则Q(x,$\frac{1}{4}{x}^{2}$+1),
代入三角形面积公式计算S△OBQ的值,化简后得二次函数并配方,计算其最小值即可.
解答  解:(1)由折叠得:CD=PD,
解:(1)由折叠得:CD=PD,
∠CDE=∠PDE,
∴∠CDQ=∠PDQ,
又 DQ=DQ,
∴△CDQ≌△PDQ,
∴CQ=PQ;
(2)如图1,∵Q(x,y),
CQ=PQ=y,
∵B(4,2),
∴BC=4,AB=2,
设QP交BC于H,则QH=y-2,CH=x,
由勾股定理,得:x2+(y-2)2=y2,
∴y=$\frac{1}{4}{x}^{2}$+1(2≤x≤4);
(3)设直线OB的解析式为:y=kx,
把B(4,2)代入得:4k=2,
k=$\frac{1}{2}$,
∴直线OB的解析式为:y=$\frac{1}{2}$x,
设直线OB与直线PQ相交于点G,设G(x,y),
则Q(x,$\frac{1}{4}{x}^{2}$+1),
∴QG=$\frac{1}{4}{x}^{2}+1-\frac{1}{2}x$,
∴S△OBQ=$\frac{1}{2}$×4×($\frac{1}{4}{x}^{2}+1-\frac{1}{2}x$)=$\frac{1}{2}{x}^{2}-x+2$=$\frac{1}{2}$(x-1)2+$\frac{3}{2}$,
当x>1时,S随x的增大而增大,
∴当x=2时,S有最小值为2.
点评 本题是四边形的综合题,考查了矩形的性质、图形与坐标特点、二次函数的最值、三角形全等的性质和判定以及勾股定理,难度适中,第一问关键证明两三角形全等,第二问关键是确定一直角三角形利用勾股定理列方程得出结论,第三问根据不规则三角形的面积等于铅直高度与水平宽度的积的一半进行计算即可.

| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
| A. | 2015 | B. | 2017 | C. | 2019 | D. | 2020 |
| 销售量y(百件) | y=-0.1x+8 | y=$\frac{120}{x}$ |
| 销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长. 如图,大圆的半径R=10,小圆的半径r=6,大圆的弦AB与小圆相切于点P,有一以点O为圆心的圆面积恰好等于圆环的面积,则它的半径等于8.
如图,大圆的半径R=10,小圆的半径r=6,大圆的弦AB与小圆相切于点P,有一以点O为圆心的圆面积恰好等于圆环的面积,则它的半径等于8.
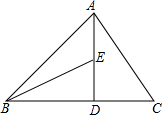 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.