题目内容
13．在实数范围内解方程$\sqrt{π-x}$+$\sqrt{x-π}$+|1-2y|=5.28，则x=π，y=2.14或-3.14．分析 根据二次根式有意义的条件可得x=π，进而可得|1-2y|=5.28，再解即可．
解答 解：由题意得：$\left\{\begin{array}{l}{π-x≥0}\\{x-π≥0}\end{array}\right.$，
解得：x=π，
∵$\sqrt{π-x}$+$\sqrt{x-π}$+|1-2y|=5.28，
∴|1+2y|=5.28，
∴1+2y=5.28或1+2y=-5.28，
解得：y=2.14或-3.14，
故答案为：π；2.14或-3.14．
点评 此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．
练习册系列答案
相关题目
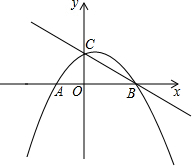如图．在平面直角坐标系中．抛物线y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2与x轴交于A、B两点，与y轴交于点C，点P从B出发．沿射线BA方向以每秒1个单位的速度匀速运动．过点P作PQ⊥x轴．直线PQ分别与直线BC、抛物线交于点Q、K．