题目内容
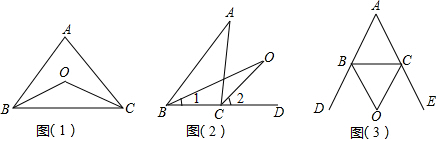
8.如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.(1)求证:⊙O与CB相切于点E;
(2)如图2,若⊙O过点H,且AC=5,AB=6,连接BO,求BO的长.

分析 (1)根据等腰三角形三线合一的性质,得CH是角平分线,根据角平分线性质得:OD=OE,根据切线的判定得出结论;
(2)连接OE,先求高线CH的长,及BH和BE的长,设未知数,根据勾股定理列方程可求得x的值,最后利用勾股定理计算即可.
解答 证明:(1)如图1,∵AC=BC,CH是高,
∴CH平分∠ACB,
∵OD⊥AC,OE⊥BC,
∴OD=OE,
∵OD是半径,
∴OE也是半径,
∴⊙O与CB相切于点E;
(2)如图2,连接OE,则OE⊥AC,
∵CH⊥AB,⊙O过点H,
∴AB与⊙O相切,
由(1)知:BC与⊙O相切,
∴BH=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
∵AC=BC=5,
∴CE=5-3=2,
由勾股定理得:CH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
设OH=x,则OE=x,OC=4-x,
则(4-x)2=x2+22,
解得x=$\frac{3}{2}$,
由勾股定理得:OB=$\sqrt{B{H}^{2}+O{H}^{2}}$=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$.
点评 本题考查了切线的性质和判定,常利用以下方法证明切线:①有垂直,证明垂线段是半径;②作垂直,证明是半径;常见的辅助线有:①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”; ②有切线时,常常“遇到切点连圆心得半径”.

练习册系列答案
相关题目
 如图,⊙O的半径是3,点P是⊙O上一点,弦AB垂直平分线段OP,点M是弧$\widehat{APB}$上的任意一点(与A、B不重合),MN⊥AB于N,以M为圆心,MN为半径作⊙M,分别过A、B作⊙M的切线,两切线交于点C.
如图,⊙O的半径是3,点P是⊙O上一点,弦AB垂直平分线段OP,点M是弧$\widehat{APB}$上的任意一点(与A、B不重合),MN⊥AB于N,以M为圆心,MN为半径作⊙M,分别过A、B作⊙M的切线,两切线交于点C.