题目内容
16.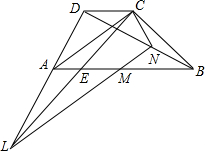 已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.
已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.
分析 延长LM至G,使LM=MG,推出四边形ALBG是平行四边形,根据平行四边形的性质得到AL=BG,AL∥GB,得到$\frac{LN}{FN}$=$\frac{DN}{BN}$,延长CN交AB于F,令LC与AB的交点为E,根据平行线分线段成比例定理得到$\frac{CN}{FN}$=$\frac{DN}{BN}$,等量代换得到$\frac{LN}{EN}$=$\frac{DN}{BN}$,推出LC∥FG,根据平行线的性质得到∠ELM=∠FGB,根据全等三角形的性质得到AE=BF,然后又全等三角形的性质结论得到结论.
解答 解:延长LM至G,使LM=MG,
∵AM=MB,LM=MG,
∴四边形ALBG是平行四边形,
∴AL=BG,AL∥GB,
∴$\frac{LN}{FN}$=$\frac{DN}{BN}$,
延长CN交AB于F,令LC与AB的交点为E,
∵AB是梯形ABCD的底边,
∴BF∥CD,
∴$\frac{CN}{FN}$=$\frac{DN}{BN}$,
由$\frac{LN}{FN}$=$\frac{DN}{BN}$,
得:$\frac{LN}{EN}$=$\frac{DN}{BN}$,
∴LC∥FG,
∴∠ELM=∠FGB,
∵AL∥GB,
∴∠LAE=∠GBF,∠ALM=∠BGM,
∴∠ALM-∠ELM=∠BGM-∠FGB,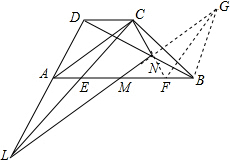
∴∠ALE=∠BGF,
在△ALE与△BGF中,$\left\{\begin{array}{l}{∠ALE=∠BGF}\\{AL=BG}\\{∠LAE=∠GBF}\end{array}\right.$,
∴△ALE≌△BGF,
∴AE=BF,
∵AC=BC,
∴∠CAE=∠CBF,
在△ACE与△BCF中,$\left\{\begin{array}{l}{AC=BC}\\{∠CAE=∠CBF}\\{AE=BF}\end{array}\right.$,
∴△ACG≌△BCF,
∴∠ACL=∠BCN.
点评 本题考查了梯形的性质,全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的判定和性质,正确的作出辅助线是解题的关键.

| A. | x1=1,x2=-3 | B. | x1=-1,x2=3 | C. | x1=-1+$\sqrt{3}$,x2=-1-$\sqrt{3}$ | D. | x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$ |
| A. | 三角形按边分可分为不等边三角形、等腰三角形 | |
| B. | 等腰三角形的内角可能是钝角或直角 | |
| C. | 三角形外角一定是钝角 | |
| D. | 三角形的中线把三角形分成面积相等的两部分 |
 如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,求当CF⊥AD时,OE的长为1.
如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,求当CF⊥AD时,OE的长为1.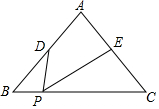 △ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4.
△ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4. 如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积. 如图,AB∥CD,AB=1,CD=4,BC=3,AD=4.
如图,AB∥CD,AB=1,CD=4,BC=3,AD=4.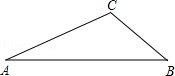 已知△ABC中,∠A=30°,AC=6.
已知△ABC中,∠A=30°,AC=6.