题目内容
6.方程x2+2x=3的根是( )| A. | x1=1,x2=-3 | B. | x1=-1,x2=3 | C. | x1=-1+$\sqrt{3}$,x2=-1-$\sqrt{3}$ | D. | x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$ |
分析 两边配上一次项系数一半的平方,写成完全平方式后再开方即可得.
解答 解:解法一:∵x2+2x=3,
∴x2+2x+1=3+1,即(x+1)2=4,
∴x+1=2或x+1=-2,
解得:x1=1,x2=-3,
解法二:∵x2+2x-3=0,
∴(x-1)(x+3)=0,
则x-1=0或x+3=0,
解得:x=1或x=-3,
故选:A.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
14.方程2x-$\sqrt{2x+3}$=3的解是( )
| A. | $\frac{1}{2}$和3 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$和3 | D. | 3 |
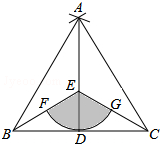 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E是AD上一点(不与点A,D重合),连接BE,CE,以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G,若BC=6,∠EBC=45°,则图中阴影部分的面积为$\frac{9}{2}$π.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E是AD上一点(不与点A,D重合),连接BE,CE,以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G,若BC=6,∠EBC=45°,则图中阴影部分的面积为$\frac{9}{2}$π. 如图,∠AOB是直角,∠AOC=40°,OD平分∠BOC,则∠AOD的度数为65°.
如图,∠AOB是直角,∠AOC=40°,OD平分∠BOC,则∠AOD的度数为65°.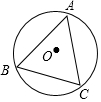 如图△ABC是⊙O的内接三角形,∠BAC=45°,BC=5,则⊙O的直径为5$\sqrt{2}$.
如图△ABC是⊙O的内接三角形,∠BAC=45°,BC=5,则⊙O的直径为5$\sqrt{2}$.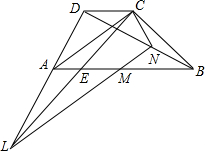 已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.
已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.