题目内容
1. 如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
分析 连结AC,在Rt△ACD中,利用勾股定理求出AD和AC的长度,然后根据已知三角形ABC的三边利用勾股定理的逆定理判定△ABC为直角三角形,最后把四边形ABCD的面积转化为两个直角三角形面积和即可求解.
解答 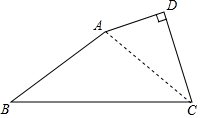 解:连结AC,
解:连结AC,
在Rt△ACD中,
∵AC2=AD2+CD2,
∴AC2=92+122,
解得:AC=15,
在△ABC中,AC=15,AB=20,BC=25,
∵AC2+AB2=BC2,
∴△ABC为直角三角形,
则S四边形ABCD=S△ACD+S△ABC=$\frac{1}{2}$×9×12+$\frac{1}{2}$×15×20=204.
即四边形土地ABCD的面积为204.
点评 本题考查了勾股定理和勾股定理的逆定理,将四边形ABCD的面积转化为两个直角三角形面积和使求解过程变得简单.

练习册系列答案
相关题目
5.某地海拔高度h与温度T的关系可用T=21-6h来表示(其中温度单位为℃,高度单位为千米),则该地区海拔高度为2000米的山顶上的温度是( )
| A. | 15℃ | B. | 3℃ | C. | -1179℃ | D. | 9℃ |
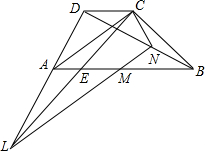 已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.
已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.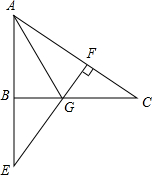 如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G.
如图,在△ABC中,∠ABC=90°,延长AB至E,使AE=AC,过E作EF⊥AC于F,EF交BC于G. 如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.
如图放置的一副直角三角板,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=2$\sqrt{3}$,则CD的长为3$\sqrt{3}$-3.