题目内容
3.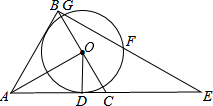 如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.(1)求证:AB与⊙O相切;
(2)若AB=4,求线段GF的长.
分析 (1)过点O作OM⊥AB,垂足是M,证明OM等于圆的半径OD即可;
(2)过点O作ON⊥BE,垂足是N,连接OF,由垂径定理得出NG=NF=$\frac{1}{2}$GF,证出四边形OMBN是矩形,在直角△OBM利用三角函数求得OM和BM的长,则BN和ON即可求得,在直角△ONF中利用勾股定理求得NF,即可得出GF的长.
解答 (1)证明:过点O作OM⊥AB,垂足是M.如图1所示: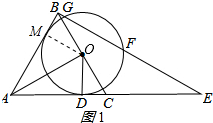
∵⊙O与AC相切于点D.
∴OD⊥AC,
∴∠ADO=∠AMO=90°.
∵△ABC是等边三角形,
∴∠DAO=∠NAO,
∴OM=OD.
∴AB与⊙O相切;
(2)解:过点O作ON⊥BE,垂足是N,连接OF.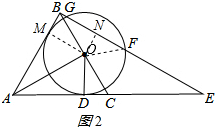 如图:2所示:
如图:2所示:
则NG=NF=$\frac{1}{2}$GF,
∵O是BC的中点,
∴OB=2.
在直角△OBM中,∠MBO=60°,
∴OM=OB•sin60°=$\sqrt{3}$,BM=OB•cos60°=1.
∵BE⊥AB,
∴四边形OMBN是矩形.
∴ON=BM=1,BN=OM=$\sqrt{3}$.
∵OF=OM=$\sqrt{3}$,
由勾股定理得:NF=$\sqrt{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{2}$,
∴GF=2NF=2$\sqrt{2}$.
点评 本题考查了切线的判定与性质、等边三角形的性质、勾股定理、垂径定理;熟练掌握切线的判定和等边三角形的性质,正确作出辅助线构造矩形是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,二次函数的图象与y轴相交于点C,与直线y=$\frac{1}{2}$x+1相交于点A、D,CD∥x轴,∠CDA=∠OCA.
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,二次函数的图象与y轴相交于点C,与直线y=$\frac{1}{2}$x+1相交于点A、D,CD∥x轴,∠CDA=∠OCA.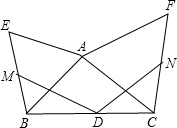 如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.
如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.