题目内容
16.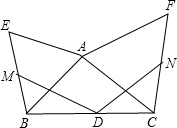 如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.
如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.
分析 连接BF、CE,由正三角形的性质得出∠BAE=∠CAF=60°,AE=AB,AC=AF,证出∠EAC=∠BAF,由SAS证明△EAC≌△BAF,得出∠AEC=∠ABF,由三角形内角和定理和对顶角相等得出∠BOG=∠BAE=60°,求出∠1+∠2=∠BOM=60°,由三角形中位线定理得出DM∥CE,DN∥BF,由平行线的性质得出∠3=∠2,∠4=∠1,求出∠3+∠4=60°,由三角形内角和定理即可得出结果.
解答 解:连接BF、CE,如图所示:
∵△ABE,△ACF均为正三角形,
∴∠BAE=∠CAF=60°,AE=AB,AC=AF,
∴∠EAC=∠BAF,
在△EAC和△BAF中,$\left\{\begin{array}{l}{AE=AB}&{\;}\\{∠EAC=∠BAF}&{\;}\\{AC=AF}&{\;}\end{array}\right.$,
∴△EAC≌△BAF(SAS),
∴∠AEC=∠ABF,
∵∠AME=∠BMC,
∴∠BOG=∠BAE=60°,
∴∠1+∠2=∠BOM=60°,
∵M,N分别为BE,CF的中点,D为△ABC的边BC的中点,
∴DE是△BCE的中位线,DN是△BCF的中位线,
∴DM∥CE,DN∥BF,
∴∠3=∠2,∠4=∠1,
∴∠3+∠4=∠1+∠2=60°,
∴∠MDN=180°-60°=120°.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质、三角形中位线定理、平行线的性质、三角形内角和定理等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
 如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).
如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).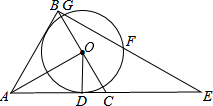 如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点. 甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).
甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).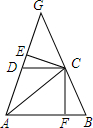 如图,△ABC中,AB∥DC,AD=DC=CH,AD,BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F,求证:DE=BF.
如图,△ABC中,AB∥DC,AD=DC=CH,AD,BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F,求证:DE=BF.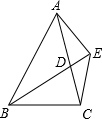 如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( )
如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( ) 如图,AB=AC,BD=DC,∠BDC=110°,求∠ADB的度数.
如图,AB=AC,BD=DC,∠BDC=110°,求∠ADB的度数.