题目内容
18. 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,二次函数的图象与y轴相交于点C,与直线y=$\frac{1}{2}$x+1相交于点A、D,CD∥x轴,∠CDA=∠OCA.
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,二次函数的图象与y轴相交于点C,与直线y=$\frac{1}{2}$x+1相交于点A、D,CD∥x轴,∠CDA=∠OCA.(1)求点C的坐标;
(2)求这个二次函数的解析式.
分析 (1)首先利用一次函数解析式计算出A、B两点坐标,然后再根据平行线的性质可得∠ACO=∠BAO,再利用三角函数可得CO长,进而可得C点坐标;
(2)首先证明△CBD∽△OBA,根据相似三角形的性质可得$\frac{BO}{CB}$=$\frac{AO}{CD}$,然后可得D点坐标,再设出二次函数解析式,利用待定系数法求出解析式即可.
解答 解:(1)∵函数y=$\frac{1}{2}$x+1中,当y=0时,x=-2,
∴A(-2,0),
∵函数y=$\frac{1}{2}$x+1中,当x=0时,y=1,
∴B(0,1),
∵CD∥x轴,
∴∠BAO=∠ADC,
∵∠CDA=∠OCA,
∴∠ACO=∠BAO,
∴tan∠ACO=tan∠BAO=$\frac{1}{2}$,
∴CO=4,
∴C(0,4);
(2)∵∠AOB=∠OCD=90°,∠BAO=∠BDC=90°,
∴△CBD∽△OBA,
∴$\frac{BO}{CB}$=$\frac{AO}{CD}$,
∴$\frac{1}{3}$=$\frac{2}{CD}$,
∴CD=6,
∴D(6,4),
设二次函数的解析式为y=ax2+bx+c,
∵图象经过A(-2,0),D(6,4),C(0,4),
∴$\left\{\begin{array}{l}{0=4a-2b+c}\\{4=c}\\{4=36a+6b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\\{c=4}\end{array}\right.$.
∴二次函数的解析式为y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4.
点评 此题主要考查了一次函数、二次函数以及相似三角形和三角函数的综合应用,关键是掌握一次函数与坐标轴交点的求法,以及待定系数法求二次函数解析式的方法.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )| A. | 从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率 | |
| B. | 任意写一个正整数,它能被2整除的概率 | |
| C. | 抛一枚硬币,连续两次出现正面的概率 | |
| D. | 掷一枚正六面体的骰子,出现1点的概率 |
 如图,已知AD=AC,请添加一个条件使得△ABC≌△AED,则可添加的条件是AB=AE.(只填写一个即可)
如图,已知AD=AC,请添加一个条件使得△ABC≌△AED,则可添加的条件是AB=AE.(只填写一个即可)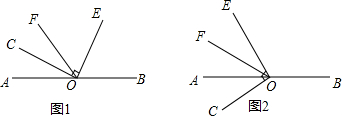
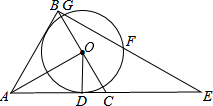 如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.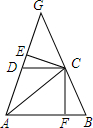 如图,△ABC中,AB∥DC,AD=DC=CH,AD,BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F,求证:DE=BF.
如图,△ABC中,AB∥DC,AD=DC=CH,AD,BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F,求证:DE=BF.