题目内容
11.已知函数y=4x2-4x+m的图象与x轴的交点坐标为(x1,0),(x2,0),且(x1+x2)(4x12-5x1-x2)=8,则该函数的最小值为( )| A. | 2 | B. | -2 | C. | 10 | D. | -10 |
分析 根据抛物线与x轴的交点问题得到x1与x2是4x2-4x+m=0的两根,由一元二次方程的解得4x12-4x1+m=0,由根与系数的关系得到x1+x2=1,x1•x2=$\frac{m}{4}$,则4x12=4x1-m,接着由(x1+x2)(4x12-5x1-x2)=8得到(x1+x2)(-m-x1-x2)=8,则1•(-m-1)=8,解得m=-9,所以抛物线解析式为y=4x2-4x-9,然后根据二次函数的性质求函数的最小值.
解答 解:∵函数y=4x2-4x+m的图象与x轴的交点坐标为(x1,0),(x2,0),
∴x1与x2是4x2-4x+m=0的两根,
∴4x12-4x1+m=0,x1+x2=1,x1•x2=$\frac{m}{4}$,
∴4x12=4x1-m,
∵(x1+x2)(4x12-5x1-x2)=8,
∴(x1+x2)(4x1-m-5x1-x2)=8,
即(x1+x2)(-m-x1-x2)=8,
∴1•(-m-1)=8,解得m=-9,
∴抛物线解析式为y=4x2-4x-9,
∵y=4(x-$\frac{1}{2}$)2-10,
∴该函数的最小值为-10.
故选D.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决本题的关键是利用一元二次方程的解的定义把4x12-5x1-x2降次.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.据平凉市旅游局统计,2015年十一黄金周期间,平凉市接待游客38万人,实现旅游收入16000000元.将16000000用科学记数法表示应为( )
| A. | 0.16×108 | B. | 1.6×107 | C. | 16×106 | D. | 1.6×106 |
 如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).
如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).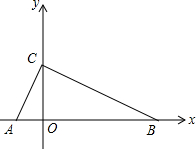 如图,已知Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴的正半轴上,且OA=1,OC=2,求经过A、B、C三点的二次函数解析式.
如图,已知Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴的正半轴上,且OA=1,OC=2,求经过A、B、C三点的二次函数解析式.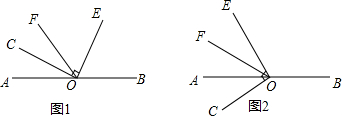
 如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.
如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.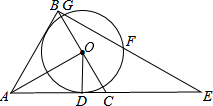 如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点. 甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).
甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).