题目内容
19. 【阅读理解】对于任意正实数a、b,因为${(\sqrt{a}-\sqrt{b})^2}$≥0,所以a-$2\sqrt{ab}+b$≥0,所以a+b≥$2\sqrt{ab}$,只有当a=b时,等号成立.
【阅读理解】对于任意正实数a、b,因为${(\sqrt{a}-\sqrt{b})^2}$≥0,所以a-$2\sqrt{ab}+b$≥0,所以a+b≥$2\sqrt{ab}$,只有当a=b时,等号成立.【获得结论】在a+b≥2$\sqrt{ab}$(a、b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,只有当a=b时,a+b有最小值2$\sqrt{p}$.
根据上述内容,回答下列问题:若m>0,只有当m=1时,m+$\frac{1}{m}$有最小值2.
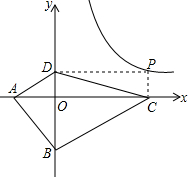
【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线$y=\frac{12}{x}(x>0)$上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
分析 (1)根据题目所给信息可知m+$\frac{1}{m}$≥2$\sqrt{m•\frac{1}{m}}$,且当m=$\frac{1}{m}$时等号成立,可得出答案;
(2)可设P(x,$\frac{12}{x}$),可表示出AC和BD,则四边形ABCD的面积为S四边形ABCD=2(x+$\frac{9}{x}$)+12,再利用所给信息可得到其最小值,此时x=3,可得出AC=BD,可得出四边形ABCD为菱形.
解答 解:
(1)根据题目所给信息可知m+$\frac{1}{m}$≥2$\sqrt{m•\frac{1}{m}}$,且当m=$\frac{1}{m}$时等号,
∴当m=1时,m+$\frac{1}{m}$≥2,
即当m=1时,m+$\frac{1}{m}$有最小值2,
故答案为:1,2;
(2)设P(x,$\frac{12}{x}$),则C(x,0),D(0,$\frac{12}{x}$),
∴CA=x+3,BD=$\frac{12}{x}$+4,
∴S四边形ABCD=$\frac{1}{2}$CA×BD=$\frac{1}{2}$(x+3)($\frac{12}{x}$+4),
化简得:S=2(x+$\frac{9}{x}$)+12,
∵x>0,$\frac{9}{x}$>0,
∴x+$\frac{9}{x}$≥2$\sqrt{x×\frac{9}{x}}$=6,
只有当x=$\frac{9}{x}$,即x=3时,等号成立,
∴S≥2×6+12=24.
∴S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),
AB=BC=CD=DA=5,
∴四边形ABCD是菱形.
点评 本题主要考查反比例函数的综合应用,涉及反比例函数解析式、菱形的判定、四边形的面积等知识点和探究问题的能力.在(1)中关键是通过对题目信息的把握,把知识应用到题目的解决中来,在(2)中关键是设出P点坐标,用x把四边形ABCD的面积表示出来,再利用题目中的结论来解决.本题为阅读理解题,这类题目主要考查学生把握信息和处理信息的能力,难度不大.

 如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( )| A. | 36 | B. | 40 | C. | $\frac{77}{2}$ | D. | 38 |
 如图,在?ABCD中,对角线AC、BD相交于O,AC+BD=10,BC=3,则△AOD的周长为8.
如图,在?ABCD中,对角线AC、BD相交于O,AC+BD=10,BC=3,则△AOD的周长为8.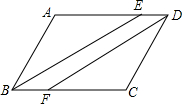 如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.
如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.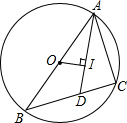 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,求tan∠CAD的值.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,求tan∠CAD的值.