题目内容
7．
如图，在?ABCD中，对角线AC、BD相交于O，AC+BD=10，BC=3，则△AOD的周长为8．
分析 由平行四边形的性质得出OA=$\frac{1}{2}$AC，OD=$\frac{1}{2}$BD，AD=BC，由已知条件得出OA+OD=5，即可求出△AOD的周长．
解答 解：∵四边形ABCD是平行四边形，
∴OA=$\frac{1}{2}$AC，OD=$\frac{1}{2}$BD，AD=BC=3，
∴OA+OD=$\frac{1}{2}$（AC+BD）=5，
∴△AOD的周长=OA+OD+AD=5+3=8；
故答案为：8．
点评 本题考查了平行四边形的性质和三角形周长的计算；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
如图，正六边形ABCDEF的边长为2，则对角线AC=2$\sqrt{3}$．
15．若把多项式x2+mx-6分解因式后含有因式x-2，则m的值为（ ）
| A． | -1 | B． | 1 | C． | ±1 | D． | 3 |
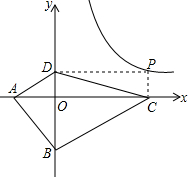【阅读理解】对于任意正实数a、b，因为${（\sqrt{a}-\sqrt{b}）^2}$≥0，所以a-$2\sqrt{ab}+b$≥0，所以a+b≥$2\sqrt{ab}$，只有当a=b时，等号成立．
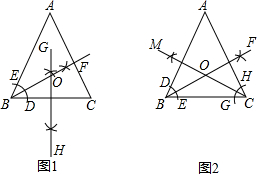△ABC中，AB=AC，在△ABC内求作一点O，使点O到三边的距离相等．