题目内容
10.已知y是x的反比例函数,且当x=4,y=-1.(1)函数y与x之间的函数表达式为y=-$\frac{4}{x}$;
(2)当一3≤x≤-$\frac{1}{2}$时,y的取值范围是$\frac{4}{3}$≤x≤8;
(3)若x>1时,y的取值范围是-4<y<0;
(4)若y<2时,x的取值范围是x>0或x<-2.
分析 (1)利用待定系数法确定反比例函数的解析式即可;
(2)根据自变量的取值范围确定函数值的取值范围即可;
(3)根据自变量的取值范围确定函数值的取值范围即可;
(4)根据函数值的取值范围确定自变量的取值范围即可.
解答 解:(1)设反比例函数的解析式为y=$\frac{k}{x}$,
∵当x=4,y=-1,
∴k=-1×4=-4,
∴反比例函数的解析式为y=-$\frac{4}{x}$;
(2)当一3≤x≤-$\frac{1}{2}$时,y=-$\frac{4}{x}$连续递增
又当x=-3时,y=$\frac{4}{3}$,当x=-$\frac{1}{2}$时,y=8,
∴当一3≤x≤-$\frac{1}{2}$时,y的取值范围是$\frac{4}{3}$≤x≤8;
(3)当x=1时,y=-4,
∵k=-4,在每一象限内y随着x的增大而增大,
∴当x>1时,y的取值范围是-4<y<0;
(4)当y=2时,x=-2,
∵k=-4,在每一象限内y随着x的增大而增大,
∴当y<2时,y的取值范围是x>0或x<-2;
故答案为:y=-$\frac{4}{x}$;$\frac{4}{3}$≤x≤8;-4<y<0;x>0或x<-2.
点评 本题考查了反比例函数的性质,求得反比例函数的解析式是解答本题的关键,注意在讨论其增减性时,需要分不同的象限讨论.

练习册系列答案
相关题目
1.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )
| A. | 105元 | B. | 210元 | C. | 170元 | D. | 不能确定 |
15.若把多项式x2+mx-6分解因式后含有因式x-2,则m的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 3 |
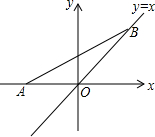 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.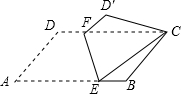 如图,将?ABCD折叠,使点A与C重合,折痕为EF.若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
如图,将?ABCD折叠,使点A与C重合,折痕为EF.若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.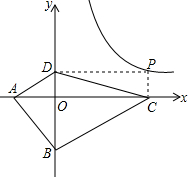 【阅读理解】对于任意正实数a、b,因为${(\sqrt{a}-\sqrt{b})^2}$≥0,所以a-$2\sqrt{ab}+b$≥0,所以a+b≥$2\sqrt{ab}$,只有当a=b时,等号成立.
【阅读理解】对于任意正实数a、b,因为${(\sqrt{a}-\sqrt{b})^2}$≥0,所以a-$2\sqrt{ab}+b$≥0,所以a+b≥$2\sqrt{ab}$,只有当a=b时,等号成立.