题目内容
11.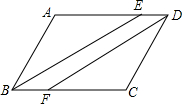 如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.
如图,四边形ABCD是平行四边形,BE平分∠ABC,DF平分∠ADC,求证:四边形DEBF是平行四边形.
分析 由四边形ABCD是平行四边形,可得AD∥BC,∠ABC=∠ADF,又由BE平分∠ABC,DF平分∠ADC,可证得∠CBE=∠CFD,即可证得BE∥DF,则可判定四边形DEBF是平行四边形.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC,
∴∠EDF=∠CFD,
∵BE平分∠ABC,DF平分∠ADC,
∴∠CBE=$\frac{1}{2}$∠ABC,∠EDF=$\frac{1}{2}$∠ADC,
∴∠CBE=∠CFD,
∴BE∥DF,
∴四边形DEBF是平行四边形.
点评 此题考查了平行四边形的判定与性质.注意有两组对角分别平行的四边形是平行四边形.

练习册系列答案
相关题目
1.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需( )
| A. | 105元 | B. | 210元 | C. | 170元 | D. | 不能确定 |
3.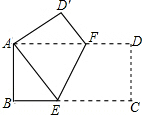 如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )
如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )
 如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )
如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与A重合,则折痕EF的长为( )| A. | 5 | B. | 6 | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
 【阅读理解】对于任意正实数a、b,因为${(\sqrt{a}-\sqrt{b})^2}$≥0,所以a-$2\sqrt{ab}+b$≥0,所以a+b≥$2\sqrt{ab}$,只有当a=b时,等号成立.
【阅读理解】对于任意正实数a、b,因为${(\sqrt{a}-\sqrt{b})^2}$≥0,所以a-$2\sqrt{ab}+b$≥0,所以a+b≥$2\sqrt{ab}$,只有当a=b时,等号成立. 如图是对某班40名学生上学出行方式调查的扇形统计图,则该班步行上学的有
如图是对某班40名学生上学出行方式调查的扇形统计图,则该班步行上学的有