题目内容
2.对于分式$\frac{x-2}{x-3}$,当x为何值时.分式的值为零?当x为何值时,分式的值大于零?当x为何值时.分式的值小于零?分析 分式的值等于0时,分子就等于0且分母不为0.分式中分子分母同号分母的值一大于0;分式中分子分母异号分式的值小于零.依此即可求解.
解答 解:分式$\frac{x-2}{x-3}$=0,x-2=0且x-3≠0,解得x=2;
分式$\frac{x-2}{x-3}$>0,$\left\{\begin{array}{l}{x-2<0}\\{x-3<0}\end{array}\right.$或$\left\{\begin{array}{l}{x-2>0}\\{x-3>0}\end{array}\right.$,解得x<2或x>3;
分式$\frac{x-2}{x-3}$<0,$\left\{\begin{array}{l}{x-2<0}\\{x-3>0}\end{array}\right.$或$\left\{\begin{array}{l}{x-2>0}\\{x-3<0}\end{array}\right.$,解得2<x<3.
答:对于分式$\frac{x-2}{x-3}$,当x=2时,分式的值为零;当x<2或x>3时,分式的值大于零;当2<x<3时,分式的值小于零.
点评 考查了分式的值为零的条件,分式的值的正负性由分子分母共同决定,分子分母同号,分式的值为正,异号分式的值为负.

练习册系列答案
相关题目
17.关于x的不等式组$\left\{\begin{array}{l}{2x<3(x-3)}\\{\frac{x+2}{2}>x+a}\end{array}\right.$ 有四个整数解,则a的取值范围是( )
| A. | -6≤a≤-$\frac{11}{2}$ | B. | -6<a≤-$\frac{11}{2}$ | C. | -6<a<-$\frac{11}{2}$ | D. | -6≤a<-$\frac{11}{2}$ |
 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2016个等腰直角三角形的斜边长是21008.
如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2016个等腰直角三角形的斜边长是21008.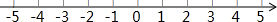 解不等式,并把解集表示在数轴上:$\left\{\begin{array}{l}{5x+7>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$.
解不等式,并把解集表示在数轴上:$\left\{\begin{array}{l}{5x+7>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$.