题目内容
7.已知关于x的不等式组$\left\{\begin{array}{l}{x-a≥b}\\{2x-a<2b+1}\end{array}\right.$的解集3≤x<5,求a2-2b.分析 分别求出每一个不等式的解集,根据不等式组的解集得到关于a、b的方程组,解方程组可得a、b的值,再代入代数式求值即可.
解答 解:解不等式x-a≥b,得:x≥a+b,
解不等式2x-a<2b+1,得:x<$\frac{a+2b+1}{2}$,
∵不等式组解集为3≤x<5,
∴$\left\{\begin{array}{l}{a+b=3}\\{\frac{a+2b+1}{2}=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=6}\end{array}\right.$,
则a2-2b
=(-3)2-2×6
=9-12
=-3.
点评 本题主要考查解一元一次不等式组、二元一次方程组、代数式的代入求值能力,正确求出不等式组的解集及解方程组是前基础,根据解集确定方程组是解题的关键.

练习册系列答案
相关题目
15.下列各式中:$\frac{4}{x}$,$\frac{a}{4}$,$\frac{1}{x-y}$,$\frac{5{π}^{2}•π}{π}$,$\frac{1}{2}{x}^{2}$,$\frac{1}{a}$-4,分式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.根据下表回答下列问题:
(1)795.24的算术平方根是28.4;
(2)$\sqrt{823.7}$≈28.7;
(3)$\sqrt{810}$在哪两个数之间?答:在28.4与28.5.
| x | 28.0 | 28.1 | 28.2 | 28.3 | 28.4 | 28.5 | 28.6 | 28.7 | 28.8 |
| x2 | 784.00 | 789.61 | 795.24 | 800.89 | 806.56 | 812.25 | 817.96 | 823.69 | 829.44 |
(2)$\sqrt{823.7}$≈28.7;
(3)$\sqrt{810}$在哪两个数之间?答:在28.4与28.5.
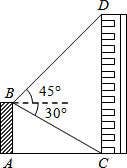 如图,某同学站在低楼AB上观察高楼CD,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,经过查找资料了解到楼房CD的高度为51.7m,求楼间距AC.($\sqrt{3}≈1.7$)
如图,某同学站在低楼AB上观察高楼CD,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,经过查找资料了解到楼房CD的高度为51.7m,求楼间距AC.($\sqrt{3}≈1.7$)