题目内容
17．关于x的不等式组$\left\{\begin{array}{l}{2x＜3（x-3）}\\{\frac{x+2}{2}＞x+a}\end{array}\right.$ 有四个整数解，则a的取值范围是（ ）| A． | -6≤a≤-$\frac{11}{2}$ | B． | -6＜a≤-$\frac{11}{2}$ | C． | -6＜a＜-$\frac{11}{2}$ | D． | -6≤a＜-$\frac{11}{2}$ |
分析 分别求出每一个不等式的解集，根据不等式组有4个整数解可得关于a的不等式组，解不等式组可得a的范围．
解答 解：解不等式2x＜3（x-3），得：x＞9，
解不等式$\frac{x+2}{2}＞x+a$，得：x＜2-2a，
∵不等式组有4个整数解，
∴13＜2-2a≤14，
解得：-6≤a＜-$\frac{11}{2}$，
故选：D．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，根据不等式组有4个整数解得到关于a的不等式组是关键．
练习册系列答案
相关题目
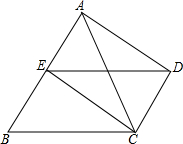已知，如图，△ABC中，E为AB的中点，DC∥AB，且DC=$\frac{1}{2}$AB，请对△ABC添加一个条件：AB=2BC，使得四边形BCDE成为菱形．
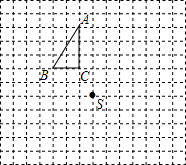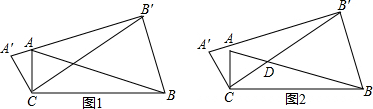
△ABC和点S都在正方形网格的格点上．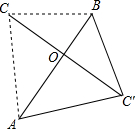
如图，△ABC的三边BC，AC，AB的长分别为3cm，4cm，5cm，把△ABC沿最长边AB翻折得到△ABC′的位置．