��Ŀ����
11��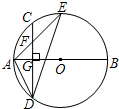 ��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�G����F��CD��һ�㣬������$\frac{CF}{FD}=\frac{1}{3}$������AF���ӳ�����O�ڵ�E������AD��DE����CF=2��AF=3���������н��ۣ��١�ADF�ס�AED����FG=2����tan��E=$\frac{\sqrt{5}}{4}$����S��DEF=4$\sqrt{5}$��������ȷ���۵ĸ����ǣ�������
��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�G����F��CD��һ�㣬������$\frac{CF}{FD}=\frac{1}{3}$������AF���ӳ�����O�ڵ�E������AD��DE����CF=2��AF=3���������н��ۣ��١�ADF�ס�AED����FG=2����tan��E=$\frac{\sqrt{5}}{4}$����S��DEF=4$\sqrt{5}$��������ȷ���۵ĸ����ǣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� ����AB�ǡ�O��ֱ������CD��AB�����ݴ��������ɵã�$\widehat{AD}$=$\widehat{AC}$��DG=CG���̶�֤�á�ADF�ס�AED��
���� $\frac{CF}{FD}$=$\frac{1}{3}$��CF=2�������DF�ij����̶����CG=DG=4��������FG=2��
���ɹ��ɶ��������AG�ij����������tan��ADF��ֵ���̶����tan��E=$\frac{\sqrt{5}}{4}$��
��������á�ADF�����������������������ıȵ������Ʊȵ�ƽ����������á�ADE��������̶����S��DEF=4$\sqrt{5}$��
��� �⣺�١�AB�ǡ�O��ֱ������CD��AB��
��$\widehat{AD}$=$\widehat{AC}$��DG=CG��
���ADF=��AED��
�ߡ�FAD=��DAE�������ǣ���
���ADF�ס�AED��
�ʢ���ȷ��
�ڡ�$\frac{CF}{FD}$=$\frac{1}{3}$��CF=2��
��FD=6��
��CD=DF+CF=8��
��CG=DG=4��
��FG=CG-CF=2��
�ʢ���ȷ��
�ۡ�AF=3��FG=2��
��AG=$\sqrt{{AF}^{2}{+FG}^{2}}$=$\sqrt{5}$��
����Rt��AGD��tan��ADG=$\frac{AG}{DG}$=$\frac{\sqrt{5}}{4}$��
��tan��E=$\frac{\sqrt{5}}{4}$��
�ʢ���ȷ��
�ܡ�DF=DG+FG=6��AD=$\sqrt{{AG}^{2}{+DG}^{2}}$=$\sqrt{21}$��
��S��ADF=$\frac{1}{2}$DF•AG=$\frac{1}{2}$��6��$\sqrt{5}$=3 $\sqrt{5}$��
�ߡ�ADF�ס�AED��
��$\frac{{S}_{��ADF}}{{S}_{��AED}}$=�� $\frac{AF}{AD}$��2��
��$\frac{3\sqrt{5}}{{S}_{��AED}}$=$\frac{3}{7}$��
��S��AED=7 $\sqrt{5}$��
��S��DEF=S��AED-S��ADF=4 $\sqrt{5}$��
�ʢ���ȷ��
��ѡD��
���� ���⿼�������������ε��ж������ʡ�Բ�ܽǶ������������������ɶ����Լ����Ǻ�����֪ʶ�������ۺ��Խ�ǿ���Ѷ����У�ע���������ν��˼���Ӧ�ã�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 4.9077��102 | B�� | 49.077��102 | C�� | 4.9077��103 | D�� | 49.077��103 |
 ��ͼ��DE�ǡ�ABC����λ�ߣ����ADE���ı���DBCE�����֮����1��3��
��ͼ��DE�ǡ�ABC����λ�ߣ����ADE���ı���DBCE�����֮����1��3�� ��ͼ��ֱ��l��������������O��A��B��OA=40cm��OB=160cm��
��ͼ��ֱ��l��������������O��A��B��OA=40cm��OB=160cm��
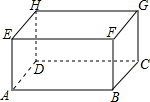 ����һ�����������߷ֱ�Ϊ5dm��4dm��3dm���dz�����ľ�䣨��ͼ��AB=5dm��BC=4dm��AE=3dm����
����һ�����������߷ֱ�Ϊ5dm��4dm��3dm���dz�����ľ�䣨��ͼ��AB=5dm��BC=4dm��AE=3dm����