题目内容
已知点A,B的坐标分别为(-1,0),(11,0),⊙B的半径为13,过点A作⊙B的弦,其中弦长为整数的共有 条.
考点:垂径定理,坐标与图形性质,勾股定理
专题:
分析:求出弦长的最小值和最大值,取其整数个数.
解答:解:∵点A,B的坐标分别为(-1,0),(11,0),⊙B半径r=13,
∴根据勾股定理易得过点A(-1,0)的最短的整数弦长为10,最长的整数弦长为26,(有一条)还有长度为11,12,…,25的各2条,
所以共有弦长为整数的1+2×15=31条.
故答案为31.
∴根据勾股定理易得过点A(-1,0)的最短的整数弦长为10,最长的整数弦长为26,(有一条)还有长度为11,12,…,25的各2条,
所以共有弦长为整数的1+2×15=31条.
故答案为31.
点评:此题考查的是垂径定理及勾股定理的应用.需注意的本题实际上是求弦长问题,容易出错的地方是:除最大弦长外,各有2条,不要漏解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB于点M,下列结论不一定成立的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点M,下列结论不一定成立的是( )| A、CM=DM | ||||
B、
| ||||
| C、∠BOD=2∠A | ||||
| D、OM=MB |
长沙地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:38,35,36,38,36,38,37,36,38,37(单位℃).则这组数据的中位数和众数分别是( )
| A、36,38 |
| B、37,38 |
| C、36.5,38 |
| D、37,36.5 |
 如图,在直线上有A、B、C、D四个点,且BC=2AB=3CD,若AD=11,那么CD=( )
如图,在直线上有A、B、C、D四个点,且BC=2AB=3CD,若AD=11,那么CD=( )| A、2 | B、3 | C、6 | D、9 |
 (1)计算:(a+2)2-a(a+4)
(1)计算:(a+2)2-a(a+4)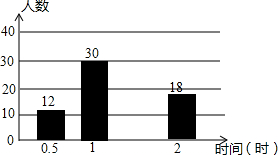 在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
 如图,△ABD中∠BAD=90°,将△ABD逆时针旋转后得到△ACE,C点落在BD边上,∠E=25°,则∠BAC=
如图,△ABD中∠BAD=90°,将△ABD逆时针旋转后得到△ACE,C点落在BD边上,∠E=25°,则∠BAC=